Question

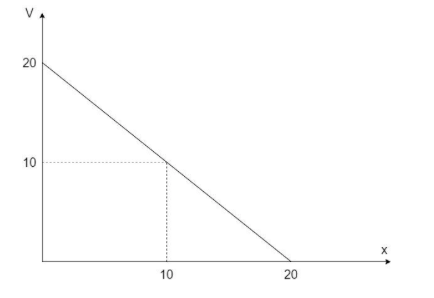
A body of mass 2 kg is moving in a straight line for which the v – x graph is shown in the figure. Magnitude of the force acting on the body at $x = 10m$ is $5k$ N. Find the value of k.

Answer 1

In this problem, the mass of the body is given. The only unknown to calculate the force is the acceleration. To find the acceleration, a relationship among the acceleration and the velocity-displacement must be deduced based on the calculus-based definitions such as:
$v = \dfrac{{dx}}{{dt}}\& a = \dfrac{{dv}}{{dt}}$
where x = displacement, v = velocity and a = acceleration.

Complete step by step solution:
The velocity of a body is defined as the rate of change of displacement per unit time. The differential form is given by:
$v = \dfrac{{dx}}{{dt}}$
Hence, we see that the velocity is a function of displacement and time.
$v = f\left( {x,t} \right)$
The acceleration of the body is the rate of change of velocity per unit time. The differential form is:
$a = \dfrac{{dv}}{{dt}} = f'\left( {x,t} \right)$

If $y = f\left( {x,t} \right)$, applying Chain rule of differentiation to the equation, we get –
$\dfrac{{dy}}{{dt}} = \dfrac{{\delta y}}{{\delta x}}\dfrac{{dx}}{{dt}} + \dfrac{{\delta y}}{{\delta t}}\dfrac{{dx}}{{dx}}$
Applying the Chain rule to the acceleration, we get –
$a = \dfrac{{dv}}{{dt}} = \dfrac{{\delta v}}{{\delta x}}\dfrac{{dx}}{{dt}} + \dfrac{{\delta v}}{{\delta t}}\dfrac{{dt}}{{dt}}$
The value $\dfrac{{\delta v}}{{\delta t}}$ , means rate of change of velocity with respect to time with displacement being constant. But, if the displacement is constant, it implies that there is no change in the velocity of the body. Hence, we get –
$\dfrac{{\delta v}}{{\delta t}} = 0$
Thus,
$a = v\dfrac{{\delta v}}{{\delta x}}$ since, $v = \dfrac{{dx}}{{dt}}$
Consider the graph of velocity v/s displacement for a body of mass 2kg as shown:

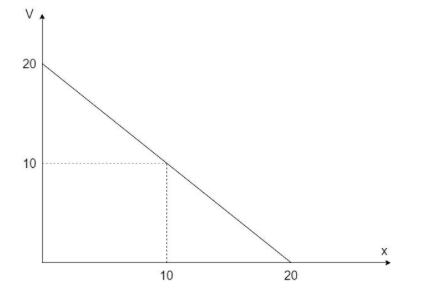
The term $\dfrac{{\delta v}}{{\delta x}}$ indicates the slope of the graph between velocity and displacement with time being constant. Now, we have a graph of velocity v/s displacement in the above equation. Hence, we can say,
$a = v \times s$
where s = slope of the graph.
The slope of the graph, $s =$ $\dfrac{{20 - 10}}{{20 - 10}} = 1$
The value of velocity at $x = 10m,v = 10m{s^{ - 1}}$
Substituting, we get –
$a = v \times s$
$a = 10 \times 1 = 10m{s^{ - 2}}$
Given the mass, $m = 2kg$
The force, $F = ma = 2 \times 10 = 20N$
Given that force, $F = 5k$, by comparing, we get –
$5k = 20 \Rightarrow k = 4$

The value of $k = 4$

Note: The students must be aware of the basic rule of calculus that – If there exists a function $y = f\left( x \right)$, i) The differential – $\dfrac{{dy}}{{dx}}$ represents the slope of the tangent to the curve
ii) The integral – $\int {y.dx}$ represents the area under the curve.