Question

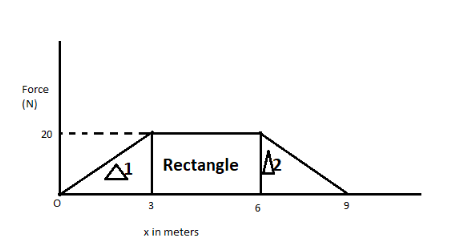
A body of mass $2.4kg$ is subjected to a force which varies with distance as shown in figure. The body starts from rest at $x = 0$. Its velocity at $x = 9$ is

A)$5\sqrt 3 m/s$
B)$20\sqrt 3 m/s$
C)$10m/s$
D)$40m/s$

Answer 1

The above question is related to the work-energy theorem. When we apply a force to anybody then its velocity changes to $v$ from $u$. If no force is applied to the body then we get no figure in the graph. But according to the graph, distance varies with time as we get the variation in the graph. So, we can easily apply the work energy theorem to solve this problem.

Formula used: - Here, we have a force which displaced the body. So, we have definite work. And also we can find the kinetic energy at different positions.
Work-energy theorem states that-‘The work done in moving a body from one position to another is equal to the difference of kinetic energies of the body at that position.’
Numerically, work energy theorem can be written as-
$W = \Delta K$
Where $\Delta K$ is the difference in the kinetic energies.
$W = {K_2} - {K_1}$...............(1)
${K_2}$ and ${K_1}$ are the kinetic energy of the body at position $2$ and position $1$ respectively.

Complete step by step solution: -
According to the graph for applying the work-energy theorem, we have to find work done by the body in $x = 0$ to $x = 9$.
Force is given i.e. $F = 20N$
So, work done is equal to the area covered by the body i.e.
Work$=$force $\times$change in displacement
$\Rightarrow work = fx$
$\Rightarrow work =$Area covered from $x = 0$ to $x = 9$
The body starts at rest, meaning $x = 0$. So, the velocity at this point is zero. It is the initial velocity of body and we are going to find final velocity gain by the body-
Kinetic energy at point $x = 0$,
${K_1} = \dfrac{1}{2}m{u^2}$
And kinetic energy at point $x = 9$,

${K_2} = \dfrac{1}{2}m{v^2}$
We know that according to the work-energy theorem

$W = {K_2} - {K_1}$
Here work is equal to the area of the graph from $x = 0$ to $x = 9$ under the influence of force $20N$.
Area in the graph consists of two triangles and one rectangle. So,
Work done$=$area of $\Delta 1 +$area of $\Delta 2 +$area of rectangle
Or we can write-
$W = \dfrac{1}{2} \times bas{e_1} \times height{t_1} + \dfrac{1}{2} \times bas{e_2} \times height{t_2} + length \times breadth$......................(ii)
Base of first triangle$= 3units(3 - 0)$
And height of first triangle$= 20N$
Similarly, base of second triangle$= 3unit(9 - 6)$
And height of second triangle$= 20N$
Base of rectangle (length)$= 3unit(6 - 3)$
Height of rectangle (breadth)$= 20unit$
So, work done from equation (i)
$\Rightarrow W = {K_2} - {K_1}$
From equation (ii), putting the value of $W$, ${K_2}$and${K_1}$.
$\Rightarrow \dfrac{1}{2} \times 3 \times 20 + \dfrac{1}{2} \times 3 \times 20 + 3 \times 20 = \dfrac{1}{2}m{v^2} - \dfrac{1}{2}m{u^2} \\\ \Rightarrow 3 \times 10 + 3 \times 10 + 3 \times 20 = \dfrac{1}{2}m{v^2} - 0 \\\$
Because the initial velocity $u$ is zero.
$\Rightarrow 30 + 30 + 60 = \dfrac{1}{2}m{v^2} \\\ \Rightarrow 120 = \dfrac{1}{2}m{v^2} \\\ \Rightarrow {v^2} = \dfrac{{120 \times 2}}{m} \\\$
Putting $m = 2.4kg$ from question.
${v^2} = \dfrac{{2 \times 120}}{{2.4}} \\\ \Rightarrow {v^2} = 100 \\\ \Rightarrow {v^2} = 10m/s \\\$
Hence, at $x = 9$, the velocity of the body will be $10m/s$.

Note: - It should be remembered that in the graph problem work done is equal to the area covered by the body and if time is given then there is no need to find the area in that case. We can directly apply Newton’s second law i.e. $F = ma$ where $a$ is acceleration, the rate of change of velocity.