Question

A body of mass 1kg is thrown up by a force of 20N. What will be its acceleration after 4s?

Answer 1

As a first step you could consider a general case where a body of mass m is thrown with force F. Then using Newton’s law you could find the net acceleration. Keep in mind that for a body thrown upwards force due to gravity is also present. Now you could simply substitute the given values for this net acceleration remains constant throughout motion.
Formula used:
Newton’s second law,
$F=ma$

Complete answer:
In the question, we are given a body of mass 1kg. This body is being thrown upwards with a force of 20N and we are asked to find the body’s acceleration after 4 seconds.
Let us discuss this situation in a general sense. Firstly let us take the case where no force is exerted on the body and the only force acting on it is that due to gravity.

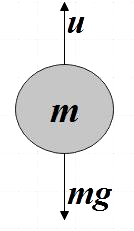
Net force here is given by,
${{F}_{net}}=mg$
From Newton’s second law,
F=ma
$\Rightarrow m{{a}_{net}}=mg$
$\Rightarrow {{a}_{net}}=g$
Hence we see that in the absence of other forces except for gravity, the body acceleration of the body remains constant and is equal to that due to gravity (g).
Now, let us discuss the case where there is the presence of external force acting on the body.

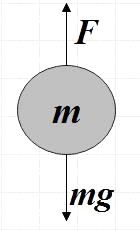
Here the body is thrown upward with a force just like the case given in the question. So here in addition to the force due to gravity we have an applied force given by,
$F=ma$
So the net force acting on the body is given by,
${{F}_{net}}=ma-mg$
$\Rightarrow m{{a}_{net}}=m\left( a-g \right)$
$\Rightarrow {{a}_{net}}=a-g$
So we see that the net acceleration on the body thrown upward with a force is constant at any instant and is given by a-g, where ‘a’ is the acceleration due to the force with which it is thrown.
Now let us discuss the case given in the question.
Here the force is 20 N, so,
$F=ma$
$\Rightarrow 20=\left( 1 \right)\times a$
$\Rightarrow a=20m{{s}^{-2}}$
The acceleration after 4s will be,
$a'=a-g$
$\Rightarrow a'=20-9.8$
$\Rightarrow a'=10.2m{{s}^{-2}}$
Therefore, for a body of mass 1kg thrown up by a force of 20N, the acceleration after 4s will be $10.2m{{s}^{-2}}$

Note:
We know that a body when thrown upwards reaches a maximum height and returns back. During this motion the magnitude of the net acceleration remains the same, however the direction of acceleration changes. That is, if (a-g) was the acceleration while moving upwards, then during downward motion, the body is accelerated with (g-a).