Question

A body of mass $1Kg$, initially at rest, explodes and breaks into three fragments of masses in the ratio $1:1:3$. The two pieces of equal mass fly off perpendicular to each other with a speed of $30m{s^{ - 1}}$ each. What is the velocity of the heavier fragment?

Answer 1

To solve this question, we should use the concept of conservation of linear momentum. We should always remember that the total or net momentum of a system is always conserved before and after any event.

Formulae used:
Law of conservation of momentum,
$momentu{m_{before}} = momentu{m_{after}}$
Here $momentu{m_{before}}$ is the momentum of the system before explosion and
$momentu{m_{after}}$ is the momentum of the system after an explosion.
$\vec p = m\vec v$
Here $\vec p$ is the momentum of the body, $m$ is the mass of the body and $\vec v$ is the velocity of the body.

Complete step by step answer:
In the question, it is given that the mass of the body was $1Kg$ and it exploded into three fragments.
Let the masses of individual fragments be ${m_1}$, ${m_2}$ and ${m_3}$. It is given in the question that the masses are in the ratio $1:1:3$. So the values of mass of each fragment is,
${m_1} = 1 \times \dfrac{1}{5} = 0.2Kg$,
${m_2} = 1 \times \dfrac{1}{5} = 0.2Kg$ and
${m_3} = 1 \times \dfrac{3}{5} = 0.6Kg$.
We know that the momentum of the system is always conserved. So,
$M\vec u = {m_1}{\vec v_1} + {m_2}{\vec v_2} + {m_3}{\vec v_3}$
Here $M$ is the mass of the particle before explosion,
$u$ is the velocity of the particle before explosion,
${m_1}$, ${m_2}$ and ${m_3}$ are the masses of the fragments after explosion and
${v_1}$, ${v_2}$ and ${v_3}$ are the velocities of the fragments after the explosion.
We know that the body is at rest before explosion as it’s already given in the question. So,
$u = 0$
$\Rightarrow 0 = {m_1}{\vec v_1} + {m_2}{\vec v_2} + {m_3}{\vec v_3}$
Substituting the values of ${m_1}$, ${m_2}$ and ${m_3}$ in the above equation, we get
$\Rightarrow 0 = 0.2{\vec v_1} + 0.2{\vec v_2} + 0.6{\vec v_3}$
$\Rightarrow {\vec v_1} + {\vec v_2} = - 3{\vec v_3}$
Let this be equation 1.
In the question, it is said that two of the particles with equal mass fly off perpendicular to each other with a speed of $30m{s^{ - 1}}$ each.

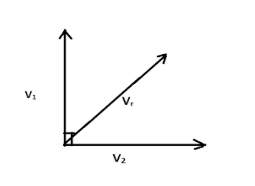
The resultant of the velocities ${v_1}$ and ${v_2}$ will be
$\Rightarrow {\vec V_r} = {\vec v_1} + {\vec v_2}$
$\Rightarrow {V_r} = \sqrt {v_1^2 + v_2^2 + {v_1}{v_2}\cos \theta } = \sqrt {{{30}^2} + {{30}^2} + \left( {30 \times 30 \times \cos 90^\circ } \right)} = 42.42m{s^{ - 1}}$
Here ${\vec V_r}$ is the resultant due to the velocities ${v_1}$ and ${v_2}$
$\theta$ is the angle between the velocities ${v_1}$ and ${v_2}$.
Equation 1 can be rewritten as,
$\Rightarrow {\vec V_r} = - 3{\vec v_3}$
$\Rightarrow {\vec v_3} = - \dfrac{1}{3}{\vec V_r}$
Let this be equation 2.
From equation 2, it is clearly evident that the velocity of the heavier particle will be one-third of the resultant velocity due to ${v_1}$ and ${v_2}$. The negative sign indicates the direction of ${v_3}$is in the opposite direction of the resultant velocity.
$\Rightarrow {v_3} = - \dfrac{1}{3}{V_r}$
$\Rightarrow {v_3} = \dfrac{1}{3} \times 42.42 = 14.14m{s^{ - 1}}$
Therefore the velocity of the heavier particle will be $14.14m{s^{ - 1}}$ in the opposite direction of the resultant of ${v_1}$ and ${v_2}$.

Note: While solving these types of questions we should be very careful about the direction given in the question as momentum is a vector quantity. Also while using the conservation of momentum equation we should consider all the particles given in the system before and after an explosion or collision.