Question

A body of mass $10\,kg$ is moving on an inclined plane of inclination $30^\circ$ with an acceleration $2\,m{\sec ^{ - 2}}$ the body starts from rest. Find the work done by force of gravity in $2\,s$
A. $10J$
B. $0$
C. $198J$
D. $196J$

Answer 1

In order to solve this question we need to understand work done and work energy theorem. Work is defined as force needed to move an object to some displacement and it is mathematically defined as $W = F.r$ . Also the work energy theorem is defined as work done by force is stored in the body in the form of energy. Work can be positive, negative or zero depending on the angle between displacement and force applied.

Complete step by step answer:
Mass of body, $m = 10kg$ and angle of inclination is $\theta = 30^\circ$. Since the body is moving with constant acceleration, we can use the equation of motion to calculate the distance it moves to move up an inclined plane.

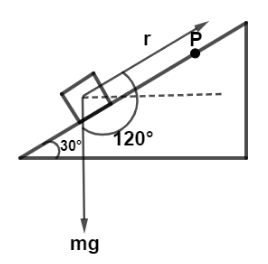
Let the distance moved be “r” by body with acceleration, $a = 2\,m{\sec ^{ - 2}}$ and in time, $t = 2\sec$ is given by
$r = ut + \dfrac{1}{2}a{t^2}$
Since the body starts from rest, $u = 0m{\sec ^{ - 1}}$.
Putting values we get,
$r = \dfrac{1}{2}(2) \times (4)$
$\Rightarrow r = 4\,m$
Now the force due to gravity is, $F = mg$.
Here “g” is acceleration due to gravity, $g = 9.8\,m\,{\sec ^{ - 2}}$

Putting values we get,
$F = (10)(9.8)N$
$\Rightarrow F = 98N$
Also the angle between displacement and force is,
$\phi = 90^\circ + 30^\circ$
$\Rightarrow \phi = 120^\circ$
So using work formula we get, $W = F.r$
$W = Fr\cos \phi$
Putting values we get,
$W = (98)(4)\cos (120)$
$\Rightarrow W = 392 \times ( - \dfrac{1}{2})$
$\therefore W = - 196J$
Here the work done is negative which shows that the work is done against gravity.

So the correct option is D.

Note: It should be remembered that here we can use the equation of motion since the acceleration is constant and uniform but if acceleration is non uniform then we have to use integration techniques or continuous distribution techniques to find the distance up to which the body moves. Also in the center of mass frame if the inclination is not fixed then it must move backward in order to conserve momentum.