Question

A body of mass 10 kg is lying on a rough horizontal surface. The coefficient of friction between the body and horizontal surface is 0.577. When the horizontal surface is inclined gradually, the body just begins to slide at a certain angle a. This is called the angle of repose. When the angle of inclination is increased further, the body slides down with some acceleration. The minimum force required just to move the body up the incline is

A. 100 N
B. 57.7
C. 11.5
D. 57.7 kg

Answer 1

This problem can be easily understood and solved using a free body diagram of the system involving the body and the surface. The minimum force required just to move the body up the incline is equal to the sum of the frictional force and the horizontal component of the normal force acting on the mass. Thus, by substituting the given values, we can find the value of the minimum force required.

Formula used:
$\mu =\tan a$
${{f}_{s}}=\mu N$

Complete step by step answer:
The free-body diagram of the system involving the mass and the surface is as shown below.

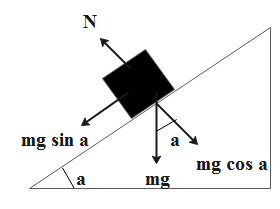
Given data as follows.
A body of mass 10 kg is lying on a rough horizontal surface.
$\Rightarrow m=10\,kg$
The coefficient of friction between the body and horizontal surface is 0.577.
$\Rightarrow \mu =0.577$
When the horizontal surface is inclined gradually, the body just begins to slide at a certain angle a.
This angle of repose can be calculated as follows.
The coefficient of friction equals the tangent of the angle of repose at which the body slides. So, we get,

& \mu =\tan a \\\ & \Rightarrow 0.577=\tan a \\\ \end{aligned}$$ Therefore, the tangent of the angle of repose is, $$\begin{aligned} & a={{\tan }^{-1}}(0.577) \\\ & \Rightarrow a\approx 30{}^\circ \\\ \end{aligned}$$ Consider the free body diagram while going through the following steps. The minimum force required just to move the body up the incline is equal to the frictional force between the body and the horizontal plane and the horizontal component of the normal force acting on the body. Firstly, compute the frictional force. $${{f}_{s}}=\mu N$$ Now, compute the force required just to move the body up the incline. $$\begin{aligned} & F={{f}_{s}}+mg\sin \,a \\\ & \Rightarrow F=\mu N+mg\sin \,a \\\ \end{aligned}$$ Continue the further calculation. $$\begin{aligned} & F=\mu mg\cos \,a+mg\sin \,a \\\ & \Rightarrow F=mg\cos \,a(\mu +\tan \,a) \\\ \end{aligned}$$ Substitute the given values in the above equation. $$\begin{aligned} & F=10\times 10\times \cos \,30{}^\circ (0.577+0.577) \\\ & \Rightarrow F=100\times \dfrac{\sqrt{3}}{2}(1.154) \\\ & \therefore F=99.93\,N \\\ \end{aligned}$$ Therefore, the minimum force required can be rounded off to the nearer decimal point as follows. F = 100 N **As the value of minimum force required just to move the body up the incline equals 100 N, thus, the option (A) is correct.** **Note:** The units of the parameters should be taken care of. In the options, the force is given in Newton and kg units, even in other units, this question can be asked. The main point to remember is that the coefficient of friction equals the tangent of the angle of repose at which the body slides.