Question

A body of mass $1\text{ }kg$ is moving with velocity $30m{{s}^{-1}}$ due north. It is acted on by a force of $10\text{ }N$ due west for $4\text{ }seconds$. Find the velocity of the body after the forced cases to act.

Answer 1

We will find the resultant velocity as one of the velocity is from X-axis and another from Y-axis, now to find the resultant we will use the Pythagoras Theorem where we form the sum of the square of the velocities to find the resultant velocity ${{V}_{r}}$ by the formula of:
${{V}_{r}}=\sqrt{{{v}^{2}}+{{V}^{2}}}$
After that we use the trigonometric identity formula of tan to find the angle of the resultant force.
$\tan \theta =\dfrac{\text{height}}{\text{base}}$
where $\theta$ is the angular direction of the motion, v is the velocity of the object from x-axis and V is the velocity of the object from y-axis.

Complete step by step answer:
Drawing a block diagram like shown below:

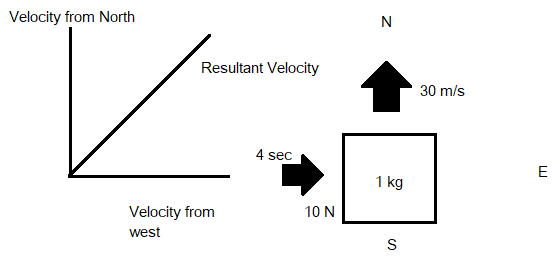
We can assume that the block is moving in the north direction with a velocity of $30m/s$.
And a force of $10N$ is exerted from the west with a certain velocity and that velocity can be calculated by calculating the value of acceleration when the force is applied from the west. Hence, to find the acceleration we use the formula:
$a\text{ }=\text{ }\dfrac{F}{m}$
Place the value of the force in the formula as $F=10N$, $m=1\text{ }kg$.
$a\text{ }=\text{ }\dfrac{10}{1}$
$a=10\text{ }m/{{s}^{2}}$
After finding the acceleration, we find the value of the velocity by using the formula of:
$v\text{ }=\text{ }u\text{ }+\text{ }at$
The initial velocity is taken as zero as the body is at rest and the final velocity is equal to the value of the product of acceleration and time taken to use the force i.e.
$v\text{ }=\text{ }0\text{ }+\text{ }10.4$
$v\text{ }=\text{ }40\text{ }m/s$
Now as we know the horizontal and vertical velocity, we find the resultant velocity as:
${{V}_{r}}=\sqrt{{{v}^{2}}+{{V}^{2}}}$
Placing v $=40$ and V $=30$, we get the value of ${{V}_{r}}$ as:
$\Rightarrow {{V}_{r}}=\sqrt{{{40}^{2}}+{{30}^{2}}}$
$\Rightarrow {{V}_{r}}=\sqrt{250}$
$\Rightarrow {{V}_{r}}=50m/s$
After finding the resultant velocity, we will find the angle at which the direction of the force is applied. To find the angle of the direction of the force applied we use the formula of $\text{tan }\theta$ as:
$\text{tan }\theta \text{= }\dfrac{\text{height}}{\text{base}}$
The velocity $40m/s$ is directed in x direction and $30m/s$ in y direction with height as $30$ and base $40$.
$\text{tan }\theta \text{= }\dfrac{\text{30}}{\text{40}}$
$\theta \text{ = ta}{{\text{n}}^{-1}}\dfrac{\text{3}}{\text{4}}$
Therefore, the resultant velocity is $50m/s$ with angle of the force applied is $\text{ta}{{\text{n}}^{-1}}\dfrac{\text{3}}{\text{4}}$.

Note:
Students may go wrong if they try to form components of the given velocity as we can find the solution through components but the value of the angle is not known and the resultant value can’t be found and another drawback is the time consumed. Hence, the process of finding the resultant directly is far more suitable.