Question

A body of mass $1\ kg$ falls from a height of $100\ m$ on a platform of mass $3\ kg$ which is mounted on a spring having spring constant $k=1.25\times {{10}^{6}}\ N/m$. The body sticks to the platform and the spring’s maximum compression is found to be x. Given that $g=10\ m/{{s}^{2}}$, the value $x$will be close to:
(a) $4\ cm$
(b) $8\ cm$
(c) $80\ cm$
(d) None of these

Answer 1

Hint: When the body falls from height h its energy will be equal to potential energy due to height which can be given as, $mgh$. Now, the body exerts force on platform due to which the spring compresses and the potential energy due to compression of spring can be given as $mgx$and all this energy is equal to the energy of spring which can be given as, $\dfrac{1}{2}k{{x}^{2}}$. Equating them we will find the value of x.

Formula used: $mgh$, $\dfrac{1}{2}k{{x}^{2}}$ , $mgx$.

Complete step by step answer:
In question it is given that a body of mass $1\ kg$ falls from a height of $100\ m$ on a platform of mass $3\ kg$ which is mounted on a spring having spring constant $k=1.25\times {{10}^{6}}\ N/m$. The body sticks to the platform and the spring’s maximum compression is found to be x and we are asked to find the value of x. So, first of all we will draw a rough figure for our simplicity,

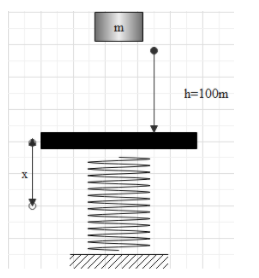
Now, when a body of any mass falls from height then its energy stored is in the form of potential energy which can be given as,
$P=mgh$
Where, m is mass, h is height and g is gravitational acceleration.
Considering the potential energy of mass $1\ kg$, for height of $100\ m$ can be given as,
${{m}_{1}}=1\ kg$
${{h}_{1}}=100\ m$
${{P}_{1}}={{m}_{1}}g{{h}_{1}}$ ………………(i)
Now, when the body of mass $1\ kg$ falls on the platform of mass $3\ kg$ is attached to spring, the spring compresses till x height, so the potential energy stored due to compression can be given as,
${{P}_{2}}=\left( {{m}_{1}}+{{m}_{2}} \right)gx$ ……………..(ii)
Here, we have considered the summation of masses of platform and body both because the potential energy acts due to the weight of both.
Now, this potential energy gets converted into kinetic energy of spring which can be seen mathematically as,
$KE=\dfrac{1}{2}k{{x}^{2}}$ ………………(iii)
Where, k is spring constant and x is displacement of spring due to compression.
Now, equating expression (i), (ii) and (iii) we will get,
${{P}_{1}}+{{P}_{2}}=KE$

${{m}_{1}}g{{h}_{1}}+\left( {{m}_{1}}+{{m}_{2}} \right)gx=\dfrac{1}{2}k{{x}^{2}}$
On substituting the values in the expression, we will get,
$\left( 1 \right)\left( 10 \right)\left( 100 \right)+\left( 1+3 \right)\left( 10 \right)x=\dfrac{1}{2}1.25\times {{10}^{6}}{{x}^{2}}$
$\Rightarrow 1000+40x=625000{{x}^{2}}$
Or $\Rightarrow 625000{{x}^{2}}-40x-1000=0$ ……………(iv)
Now, the standard quadratic equation can be given as, $a{{x}^{2}}+bx+c=0$
To find the roots the equation can be written as, $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Comparing expression (iv) with standard equation, the values of a, b and c can be given as,
$a=625000$
$b=-40$
$c=-1000$
Substituting these values in the expression of roots we will get,
$x=\dfrac{-\left( -40 \right)\pm \sqrt{{{\left( -40 \right)}^{2}}-4\left( 625000 \right)\left( -1000 \right)}}{2\left( 62500 \right)}$
Solving the expression, the value of x can be given as,
$x=0.04\ m$ or $x=-0.039\ m$
$x=4\ cm$ or $x=-3.9\ cm\simeq -4\ cm$
Here, both the values are same in magnitude only the sign changes. As there is compression in the spring we can consider $-3.9\ cm$ as our answer, but the options are in magnitude so we can neglect the sign, so the final answer will be $x=4\ cm$.
Thus, option (a) is the correct answer.

Note: Here in the question the mass of spring is not given so we are neglecting its mass while calculating the potential energy stored in the spring. But if mass of spring is given something then our expression (ii) will become, ${{P}_{2}}=\left( {{m}_{1}}+{{m}_{2}}+{{m}_{3}} \right)gx$and the answer will also change. So, students must read the given data carefully and work accordingly.