Solveeit Logo
Login

Question

Question: A body of mass \(0.5Kg\) is projected under gravity with a speed of \(98m/s\)at an angle of \(30^\ci...

A body of mass 0.5Kg0.5Kg is projected under gravity with a speed of 98m/s98m/sat an angle of 30∘30^\circ with the horizontal. The change in momentum (in magnitude) of the body when its strike the ground is
A. 98 N - s98{\text{ N - }}s
B. 49 N - s49{\text{ N - }}s
C. 196 N - s196{\text{ N - }}s
D. 24.5 N - s24.5{\text{ N - s}}

Explanation

Solution

Concept of final and initial velocity of a projectile thrown at an angle with the horizontal and change in momentum which is both horizontal change in momentum and vertical change in momentum.
(1). Momentum, P=P = mass×\timesvelocity
(2). Change in momentum ==final momentum –– Initial momentum

Complete step by step answer:

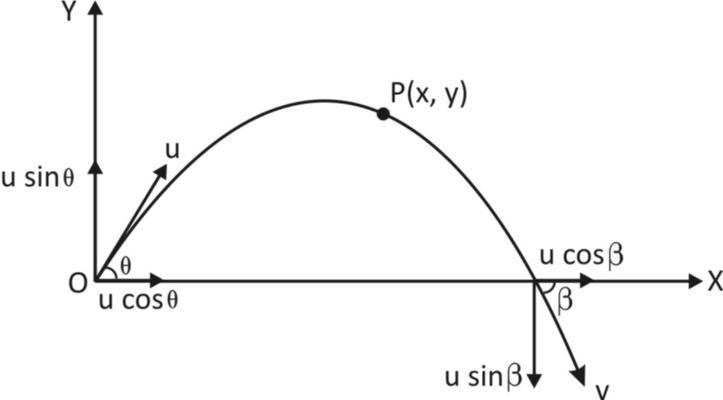
Let us consider a projectile as shown in the figure with initial velocity vvat an angle θ\theta with the horizontal.
Let it finally hit the ground after time of flight, ttwith final velocity vvmaking an angle β\beta with the horizontal.
Now, let at any instant, tt, when the body is at point P(x,y)P\left( {x,y} \right)velocity, vvwill have two rectangular components.
Horizontal component of velocity,
vx=ucos⁡θ{v_x} = u\cos \theta …….. (as ax=0{a_x} = 0)
And vertical component of velocity,
vy=usin⁡θ−gt{v_y} = u\sin \theta - gt……….. (Using v=u+atv = u + at and a=−ga = - g)
Resultant velocity at pointPP,

v=vx2+vy2=(ucos⁡θ)2+(usin⁡θ−gt)2 v=u2+g2t2−2ugtsin⁡θ  v = \sqrt {v{x^2} + v{y^2}} = \sqrt {{{\left( {u\cos \theta } \right)}^2} + {{\left( {u\sin \theta - gt} \right)}^2}} \\\ v = \sqrt {{u^2} + {g^2}{t^2} - 2ugt\sin \theta } \\\

At end point, t=t = time of flight t=2usin⁡θgt = \dfrac{{2u\sin \theta }}{g}
So,

v=u2+g2(2usin⁡θg)−2ug(2usin⁡θg)sin⁡θ =u2=u  v = \sqrt {{u^2} + {g^2}\left( {\dfrac{{2u\sin \theta }}{g}} \right) - 2ug\left( {\dfrac{{2u\sin \theta }}{g}} \right)\sin \theta } \\\ = \sqrt {{u^2}} = u \\\

⇒\RightarrowFinal velocity ==initial velocity
If velocity makes angle β\beta with the horizontal, then
tan⁡β=vyvx=usin⁡θ−gtucos⁡θ tan⁡β=usin⁡θ−g⋅2usin⁡θgucos⁡θ tan⁡β=−usin⁡θucos⁡θ=−tan⁡θ=tan⁡(−θ) β=−θ  \tan \beta = \dfrac{{{v_y}}}{{{v_x}}} = \dfrac{{u\sin \theta - gt}}{{u\cos \theta }} \\\ \tan \beta = \dfrac{{u\sin \theta - g \cdot \dfrac{{2u\sin \theta }}{g}}}{{u\cos \theta }} \\\ \tan \beta = - \dfrac{{u\sin \theta }}{{u\cos \theta }} = - \tan \theta = \tan \left( { - \theta } \right) \\\ \beta = - \theta \\\
So, direction changes
Now, horizontal change in
Momentum =mvx−mux = m{v_x} - m{u_x}

=mvcos⁡β−mucos⁡θ =mucos⁡(−θ)−mucos⁡θ \-(as v=u, θ=−β) =mucos⁡θ−mucos⁡θ =0  = mv\cos \beta - mu\cos \theta \\\ = mu\cos \left( { - \theta } \right) - mu\cos \theta \\\ \- \left( {as{\text{ v}} = u,{\text{ }}\theta = - \beta } \right) \\\ = mu\cos \theta - mu\cos \theta \\\ = 0 \\\

So, no horizontal change in momentum vertical change in momentum
=mvy−muy =mvsin⁡β−musin⁡θ =musin⁡(−θ)−musin⁡θ =−musin⁡θ−musin⁡θ =−2musin⁡θ  = m{v_y} - m{u_y} \\\ = mv\sin \beta - mu\sin \theta \\\ = mu\sin \left( { - \theta } \right) - mu\sin \theta \\\ = - mu\sin \theta - mu\sin \theta \\\ = - 2mu\sin \theta \\\
So, net change in momentum is the sum of both.
Net change in momentum =∣−2musin⁡θ∣ = \left| { - 2mu\sin \theta } \right|
Here m=0.5Kg, u=98m/s θ=30∘  m = 0.5Kg,{\text{ }}u = 98m/s \\\ \theta = 30^\circ \\\
So, change in momentum =∣−2×0.5×98×sin⁡30∣ = \left| { - 2 \times 0.5 \times 98 \times \sin 30} \right|
=2×12×98×12 =982 =49Ns  = 2 \times \dfrac{1}{2} \times 98 \times \dfrac{1}{2} \\\ = \dfrac {{98}}{2} \\\ = 49Ns \\\

So, the correct answer is “Option B”.

Note:
Here we have found only the magnitude of net change in momentum, so we can ignore negative signs. Also as there is no net horizontal acceleration to the body projected so change in horizontal velocity will be zero and hence change in horizontal momentum is also zero while in vertical direction, acceleration due to gravity occurs in vertically downward direction to which vertical change in momentum corresponds.