Solveeit Logo
Login

Question

Question: A body of density \[\rho \] is dropped from rest from a height h into a lake of density \[\sigma ,\l...

A body of density ρ\rho is dropped from rest from a height h into a lake of density σ,(σ>ρ)\sigma ,\left( \sigma >\rho \right). The maximum depth the body sinks inside the liquid is (neglect viscous effect of liquid):
A. hρσ−ρ\dfrac{h\rho }{\sigma -\rho }
B. hσσ−ρ\dfrac{h\sigma }{\sigma -\rho }
C. hρσ\dfrac{h\rho }{\sigma }
D. hσρ\dfrac{h\sigma }{\rho }

Explanation

Solution

In this question we have been asked to calculate the maximum depth a body will sink in the liquid when dropped from height ‘h’. It is given that the density of the body is ρ\rho and the density of the lake is σ\sigma . We know that, if an object is dropped in liquid, the object will float or sink in the lake due to the amount of Buoyancy force. Therefore, to calculate the depth we shall first calculate the force acting on the body after it is dropped in the lake.

Formula used:
v2=u2+2as{{v}^{2}}={{u}^{2}}+2as

Complete solution:
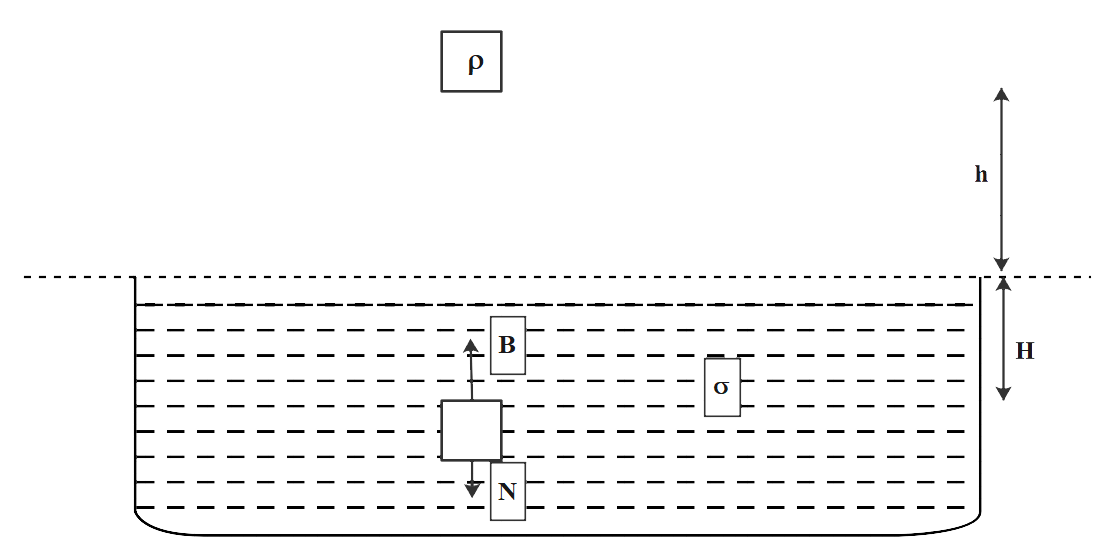
It is given that the body is dropped from a height ‘h’ into a lake. Now, let us assume that the body sinks to a height of ‘H’ as shown in the figure.

Now, from second kinematic equation
We know,
v2=u2+2as{{v}^{2}}={{u}^{2}}+2as ……………… (1)
Since the velocity of the body is at rest u = 0. The body is falling due to gravity, therefore a = g
After substituting the values
We get,
v2=0+2gh{{v}^{2}}=0+2gh
Therefore,
v=2ghv=\sqrt{2gh} ……………. (2)
Now, we know that mass of a body can be given as the product of density of the body and its volume. Therefore, the force N is given as,
N=ρVgN=\rho Vg
From the diagram, the buoyant force is B is given as,
B=σVgB=\sigma Vg
From diagram we can say that,
F=B−NF=B-N
After substituting the values
We get,
F=σVg−ρVgF=\sigma Vg-\rho Vg
We can also write,
ρVa=σVg−ρVg\rho Va=\sigma Vg-\rho Vg ………….. (∵\because F=ma; m=density×\times volume)
Solving for ‘a’
We get,
a=g(σ−ρρ)a=g\left( \dfrac{\sigma -\rho }{\rho } \right) …………….. (3)
Now, we know that when the body will be at rest when it is submerged in liquid at depth ‘H’ as shown in the figure.
Therefore,
From (1) and (3)
We get,
0=(2gh)2−2g(σ−ρρ)×H0={{\left( \sqrt{2gh} \right)}^{2}}-2g\left( \dfrac{\sigma -\rho }{\rho } \right)\times H
Therefore,
H=(hρσ−ρ)H=\left( \dfrac{h\rho }{\sigma -\rho } \right)

Therefore, the correct answer is option A.

Note:
The kinetic equation also known as kinematic equation is a set of equations that are used to define the motion of a body moving with constant acceleration. The three kinetic equations give the relation between distance, final and initial speeds and acceleration of a particle. The kinetic equations are very useful to calculate the velocity or acceleration of a particle provided other quantities are provided.