Question

A body of density ${{d}_{1}}$ is counterpoised by Mg of weights of density ${{d}_{2}}$ in air of density d. Then the true mass of the body is
A. M
B. $M\left( 1-\dfrac{d}{{{d}_{2}}} \right)$
C. $M\left( 1-\dfrac{d}{{{d}_{1}}} \right)$
D. $\dfrac{M\left( 1-d/{{d}_{1}} \right)}{\left( 1-d/{{d}_{2}} \right)}$

Answer 1

Here, we calculate the apparent weight of the body in terms of its density, by subtracting the up-thrust due to displaced air by the original weight of the body. The apparent weight of a mass M is calculated using the same method. Now, it is given that weight of the body is counterpoised, that is, balanced by the mass, M. Hence, the apparent weight of both can be equated and on simplifying the equation, we can obtain the true mass of the body.
Formula used:
Apparent weight of a body is given by,
$mg-Vdg$
where, mg is the actual weight of the body, V is volume of the body, d is density of the medium and g is acceleration due to gravity.
Volume of a body is given by,
$V=\dfrac{m}{d}$
where, m is mass of the body and d is density of the body.

Complete answer:

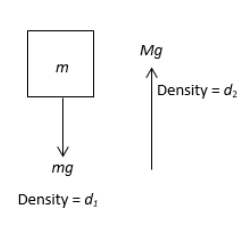
Let the true mass of the body be m.
Apparent weight of the body is given by,
$mg-Vdg$
Since, density of the body is ${{d}_{1}}$, therefore,
$V=\dfrac{m}{{{d}_{1}}}$
Substituting this value in the apparent weight of body, we get,
Apparent weight of the body = $mg-\left( \dfrac{m}{{{d}_{1}}} \right)dg$
Simplifying the above expression, we get,
$\text{ }mg-\left( \dfrac{m}{{{d}_{1}}} \right)dg$
$\Rightarrow m\left( 1-\dfrac{d}{{{d}_{1}}} \right)g$
Now, apparent weight of the mass is given by,
$Mg-Vdg$
Since, density of the mass is ${{d}_{2}}$, therefore,
$V=\dfrac{M}{{{d}_{2}}}$
Substituting this value in the apparent weight of mass, we get,
Apparent weight of mass = $Mg-\left( \dfrac{M}{{{d}_{2}}} \right)dg$
Simplifying the above expression, we get,
$\text{ M}g-\left( \dfrac{M}{{{d}_{2}}} \right)dg$
$\Rightarrow M\left( 1-\dfrac{d}{{{d}_{2}}} \right)g$
Now, apparent weight of the body will be equal to the apparent weight of the mass, therefore,
$m\left( 1-\dfrac{d}{{{d}_{1}}} \right)g=M\left( 1-\dfrac{d}{{{d}_{2}}} \right)g$
Simplifying the above equation to find the true mass (m) of the body, we get,
$m=\dfrac{M\left( 1-\dfrac{d}{{{d}_{2}}} \right){g}}{\left( 1-\dfrac{d}{{{d}_{1}}} \right){g}}$
$m=\dfrac{M\left( 1-d/{{d}_{2}} \right)}{\left( 1-d/{{d}_{1}} \right)}$

Therefore, none of the options are correct.

Note:
If the force of buoyancy on the object would have been greater than the weight of the object, then, the apparent weight of the object would have been negative. Also, the apparent weight of an object in water is less than that in air.