Question

A body moves over one fourth of a circular arc in a circle of radius $r$. The magnitude of distance travelled and displacement will be respectively
A. $\dfrac{{\pi r}}{2},r\sqrt 2$
B. $\dfrac{{\pi r}}{4},r$
C. $\pi r,\dfrac{r}{{\sqrt 2 }}$
D. $\pi r,r$

Answer 1

Use the formula for the circumference of the circle. The distance travelled by the particle is the total distance travelled by the particle and displacement of the particle is the shortest distance between the initial and final position of the particle. Hence, determine the distance travelled by taking one fourth of the circumference of the circle and displacement using Pythagoras theorem.

Formula used:
The circumference $C$ of a circle is given by
$C = 2\pi r$ …… (1)
Here, $r$ is the radius of the circle.

Complete step by step answer:
We have given that a body moves on the circumference of the circle and travels the distance one fourth of the circular arc of radius $r$. We have asked to determine distance travelled and displacement of the body during this travel.

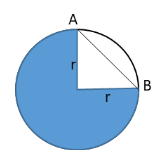
In the above diagram, the body moves from point A to B to cover one fourth of the circular path.Let us first determine the distance travelled by the body.The distance $d$ travelled is equal to one fourth of the circumference $C$ of the circular path.
$d = \dfrac{1}{4}\left( {2\pi r} \right)$
$\Rightarrow d = \dfrac{{\pi r}}{2}$
Hence, the distance travelled by the body is $\dfrac{{\pi r}}{2}$.

Let us now determine the displacement of the body.The displacement of the body is the shorted distance between the initial and final point of the travel.In the present case, the displacement of the body is the distance between the line joining points A and B. We can determine this distance between the points A and B using Pythagoras theorem.Let us apply Pythagoras theorem to the triangle formed by the motion of the body.
${\text{A}}{{\text{B}}^2} = {r^2} + {r^2}$
$\Rightarrow {\text{A}}{{\text{B}}^2} = 2{r^2}$
$\therefore {\text{AB}} = r\sqrt 2$
Hence, the displacement of the body is $r\sqrt 2$. Therefore, the distance travelled and displacement of the body are $\dfrac{{\pi r}}{2}$ and $r\sqrt 2$ respectively.

Hence, the correct option is A.

Note: The students should be careful while determining the distance travelled and displacement of the body. One should not get confused between the concepts distance travelled and displacement of the body. If one gets confused between these two concepts then the final answer to the question will be incorrect.