Question
Question: A body moves from rest with a constant acceleration. Which one of the following graphs represents th...
A body moves from rest with a constant acceleration. Which one of the following graphs represents the variation of its kinetic energy K with the distance travelled (x)?
A.
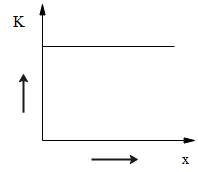
B.
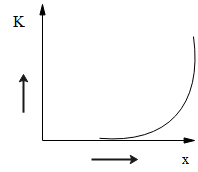
C.
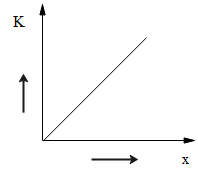
D.
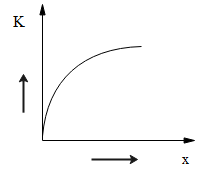
Explanation
Solution
We will make use of the formulae like the kinetic energy of the particle and one of the laws of motion equations to solve this graphical problem. We will derive the expression using these equations, such that, the equation represents the relation between the kinetic energy K with the distance travelled (x), which is needed to determine the type of graph.
Formula used:
& K=\dfrac{1}{2}m{{v}^{2}} \\\ & {{v}^{2}}={{u}^{2}}+2as \\\ \end{aligned}$$ **Complete step-by-step answer:** The formulae used are as follows: The kinetic energy of the body is given as follows. $$K=\dfrac{1}{2}m{{v}^{2}}$$…… (1) Where m is the mass of the body and v is the velocity of the body. The law of motion formula is given as follows. $${{v}^{2}}={{u}^{2}}+2as$$…… (2) Where v is the final velocity of the body, u is the initial velocity of the body, a is the acceleration and s is the distance travelled. From given, we have the data as follows: A body moves from rest with a constant acceleration. $$\begin{aligned} & \Rightarrow u=0 \\\ & \Rightarrow a=a \\\ \end{aligned}$$ The distance travelled is x $$\Rightarrow s=x$$ Substitute these values in the equation (2) $$\begin{aligned} & {{v}^{2}}={{(0)}^{2}}+2(a)(x) \\\ & \Rightarrow {{v}^{2}}=2ax \\\ \end{aligned}$$ Now substitute this value of the final velocity in the expression of the kinetic energy of the body given in the equation (1). So, we get, $$\begin{aligned} & K=\dfrac{1}{2}m(2ax) \\\ & \Rightarrow K=\max \\\ \end{aligned}$$ Therefore, the relation between the kinetic energy and the distance travelled by the body is given to be, $$\begin{aligned} & K=(\operatorname{ma})x \\\ & \Rightarrow K\propto x \\\ \end{aligned}$$ Thus, the kinetic energy and the distance travelled are directly proportional to each other. As the kinetic energy and the distance travelled are directly proportional to each other, thus, the option (C) is correct. **So, the correct answer is “Option (C)”.** **Note:** In order to solve these types of questions, the formulae or the equations that can be used to determine the relationship between the energies and the parameters of the motion should be known. Here, the relation between the kinetic energy and the distance travelled is asked, even they can ask the relation between the other parameters mentioned above.