Question

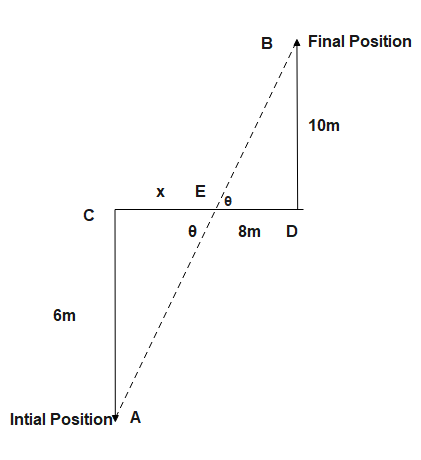
A body moves $6 \mathrm{~m}$ north, $8 \mathrm{~m}$ east and $10 \mathrm{~m}$ vertically upwards, What is its resultant displacement from initial position:
A.$10\sqrt{2}~\text{m}$
B.$10 \mathrm{~m}$
C.$\dfrac{10}{\sqrt{2}}~\text{m}$
D.$10 \times 2 \mathrm{~m}$

Answer 1

The result is a resultant displacement when displacement vectors are added. But as long as they are the same vector quantity, any two vectors can be added. If two or more velocity vectors are added, the resulting velocity is the result. Calculate the shortest distance between the initial and the final position of the body A to B by the help of the Resultant vector.

Complete answer:

The sum of the two displacements having the same direction as the original vectors is the resulting one. The result is the sum of the two displacements having the opposite direction to the original vectors' direction. If two or more force vectors are added, the outcome is a resultant force. Displacement is a quantity of a vector that refers to "how far out of place an object is"; it is the overall position change of the object.
Consider that the east direction is x-direction, the north direction is y-direction, and the z-direction is vertically upward. The Distance and Displacement SI Unit is the metre
Displacement of the particle is given by
$\overrightarrow{\mathrm{S}}=8 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}+10 \hat{\mathrm{k}}$
Magnitude of displacement
$|\overrightarrow{\mathrm{S}}|=\sqrt{6^{2}+8^{2}+10^{2}}=10 \sqrt{2} \mathrm{~m}$
Its resultant displacement from initial position is $|\overrightarrow{\mathrm{S}}|=\sqrt{6^{2}+8^{2}+10^{2}}=10 \sqrt{2} \mathrm{~m}$

The correct option is (A) .

Note:
Distance is the length of an object's path, while displacement is simply the distance between where and where the object started. Let's say you drive a car, for instance. Five miles east and then three miles west, you drive it. Also, the minimum distance between the starting and final positions is displacement.