Question

A body is simultaneously given two velocities, one $30m{s^{ - 1}}$ due east and other $40m{s^{ - 1}}$ due north. Find the resultant velocity.

Answer 1

Here in this question we have to find the resultant velocity and for this by using the Pythagoras theorem we can easily solve this question. As while following the instruction from the question we have a right angled triangle. So this concept will be used to get the resultant velocity.

Complete step by step answer: So let us suppose a body has started moving from the point $O$ and then according to the question body went towards the east with the velocity $30m{s^{ - 1}}$ and from there the body went due north with the velocity $40m{s^{ - 1}}$ . From this we have the figure, as

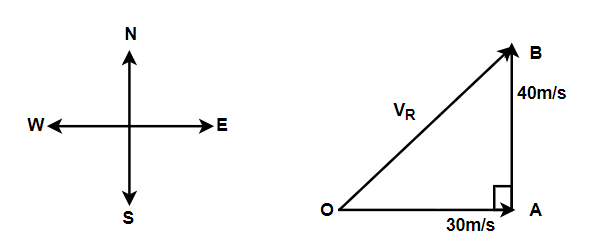
Therefore, in right angled $\vartriangle OAB$ ,
The resultant velocity equal to,
$\Rightarrow {V_{\vec R}} = \sqrt {{{\left( {30} \right)}^2} + {{\left( {40} \right)}^2}}$
And on solving it, we get
$\Rightarrow {V_{\vec R}} = \sqrt {900 + 1600}$
And on adding it, we get
$\Rightarrow {V_{\vec R}} = \sqrt {2500}$
And on solving the square root, we get
$\Rightarrow {V_{\vec R}} = 50m/s$

Therefore, the resultant velocity is equal to $50m/s$ .
Note: For solving this type of question, it’s better to first draw the direction and then proceed with the question statement. As it decreases the chances of error while solving it. If we follow these two above points then we can easily solve such types of questions.