Question

A body is released from a point of distance ($R'$) from the center of earth. Its velocity at the time of striking the earth will be ($R' > {R_e}$).

Answer 1

Hint: In this particular type of question use the concept that according to conservation of energy, initial energy should be equal to the final energy and the final energy is the sum of final gravitational potential energy and the kinetic energy of the body so use these concepts to reach the solution of the question.

Complete answer:

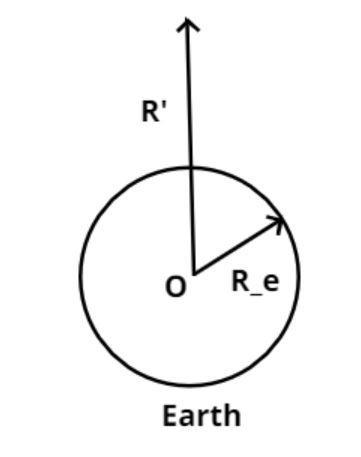
Let the center of the earth be O as shown in the figure.
Radius of the earth is ${R_e}$units
And a body is at a point R units from the center of the earth as shown in the figure.
Given (R’>${R_e}$) so the point is above the earth surface as shown in the figure.
Let (m) be the mass of the body and (M) be the mass of the earth.
So when the body released the kinetic energy of the body is given as,
$\Rightarrow K.E = \dfrac{1}{2}m{v^2}$, where (v) is the velocity of the body.
Now as we know that the gravitational potential energy between two bodies is given as,
Gravitational potential energy = $- \dfrac{{GmM}}{R}$, where G = universal gravitational constant, m = mass of the first body, M = mass of the other object and R = distance between them.
Now by conservation of energy we have,
Initial energy = final energy
Initial Gravitational potential energy = final Gravitational potential energy + kinetic energy.
Therefore,
$\Rightarrow - \dfrac{{GmM}}{{R'}} = - \dfrac{{GmM}}{{{R_e}}} + \dfrac{1}{2}m{v^2}$
Now cancel out m from both the sides we have,
$\Rightarrow - \dfrac{{GM}}{{R'}} = - \dfrac{{GM}}{{{R_e}}} + \dfrac{1}{2}{v^2}$
$\Rightarrow \dfrac{1}{2}{v^2} = \dfrac{{GM}}{{{R_e}}} - \dfrac{{GM}}{{R'}}$
$\Rightarrow {v^2} = 2GM\left[ {\dfrac{1}{{{R_e}}} - \dfrac{1}{{R'}}} \right]$
$\Rightarrow {v^2} = \dfrac{{2GM}}{{{R_e}}}\left[ {1 - \dfrac{{{R_e}}}{{R'}}} \right]$
Now take square root on both sides we have,
$\Rightarrow v = \sqrt {\dfrac{{2GM}}{{{R_e}}}\left[ {1 - \dfrac{{{R_e}}}{{R'}}} \right]}$.................. (1)
Now as we know that the weight of an object is equal to the force exerted on an object by the earth.
Weight of an object = mg
And the force exerted on the body by the earth = $G\dfrac{{mM}}{{R_e^2}}$
Therefore, $mg = G\dfrac{{mM}}{{R_e^2}}$
$\Rightarrow gR_e^2 = GM$
Now substitute this value in equation (1) we have,
$\Rightarrow v = \sqrt {\dfrac{{2gR_e^2}}{{{R_e}}}\left[ {1 - \dfrac{{{R_e}}}{{R'}}} \right]}$
$\Rightarrow v = \sqrt {2g{R_e}\left[ {1 - \dfrac{{{R_e}}}{{R'}}} \right]}$
So this is the required velocity of the body at the time of striking the earth.
Hence option (D) is the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall the formula for the gravitational potential energy, kinetic energy, weight of the body and the force exerted on the body by the earth which is all stated above, these will help us to find out the right answer of the given problem.