Question

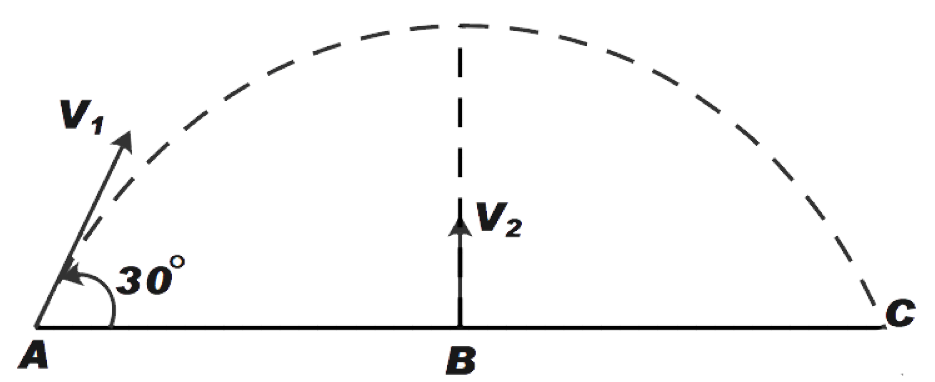
A body is projected with a velocity ${{V}_{1}}$ from the point A as shown in the figure. At the same time another body is projected vertically upwards from B with velocity ${{V}_{2}}$. The point B lies vertically below the highest point. For the bodies to collide $\dfrac{{{V}_{2}}}{{{V}_{1}}}$ should be

A. 2
B. 0.5
C. $\sqrt{\dfrac{3}{2}}$
D. 1

Answer 1

In this question we have been asked to calculate the ratio of velocities of two bodies projected from Points A and B such that their paths intersect and they collide with each other. Now, we know that the particles will only collide when the body projected from point A reaches its maximum height above point B from where the other body is projected vertically upwards. Therefore, we will be using the equation of motion to solve this problem.

Complete answer:
As shown in the figure, the body from point A will collide with the particle projected vertically upward from point B, at the maximum height of the projectile, which is given to be above the point B. Now, we know that the vertical distance covered by both points will be equal.
Therefore, we will now calculate the vertical distance travelled by body projected from point A.
We know from equation of motion that,
$S=ut+\dfrac{1}{2}a{{t}^{2}}$
Therefore, the vertical distance i.e. distance along y axis will be given by,
${{S}_{y}}={{u}_{y}}t+\dfrac{1}{2}{{a}_{y}}{{t}^{2}}$
Now, we know that for a body in projectile motion the velocity along Y-axis is given as ${{u}_{y}}={{V}_{1}}\sin 30{}^\circ$, let us assume the maximum height is H
Therefore,
We get,
$H={{V}_{1}}\sin 30{}^\circ t-\dfrac{1}{2}g{{t}^{2}}$ ……………. (1)
Now, the vertical distance travelled by body projected from point B
Therefore,
$S=ut+\dfrac{1}{2}a{{t}^{2}}$
After substituting values
We get,
$H={{V}_{2}}t-\dfrac{1}{2}g{{t}^{2}}$ ………………. (2)
Now, from (1) and (2)
We can say,
${{V}_{1}}\sin 30{}^\circ t-\dfrac{1}{2}g{{t}^{2}}={{V}_{2}}t-\dfrac{1}{2}g{{t}^{2}}$
Now, we know that if the bodies are to collide the time taken by both the bodies will be equal
Therefore, we can say,
${{V}_{1}}\sin 30{}^\circ ={{V}_{2}}$
Therefore,
$\dfrac{{{V}_{2}}}{{{V}_{1}}}=\sin 30{}^\circ$
We know $\sin 30{}^\circ =\dfrac{1}{2}=0.5$
Therefore,
$\dfrac{{{V}_{2}}}{{{V}_{1}}}=0.5$
Therefore, the correct answer is option B.

Note:
When an object is thrown or projected at some angle with the horizontal, the motion of the object is known as projectile motion. The object is known as the projectile and the path followed by the projectile is known as trajectory. In projectile motion after the body is projected, the body is only subjected to gravitational force. Therefore, after reaching the maximum height in trajectory, the projectile starts descending in a downward curve under gravity.