Question

A body is projected with a velocity of $40m/s$ . After $2\operatorname{s}$ if crosses a vertical pole of height $20cm$ . Calculate the angle of projection and horizontal range.

Answer 1

When a body is projected at a certain angle with the ground as a reference then it experiences a projectile motion and follows a parabolic path. The height and range achieved by the body in a projectile motion depend on the angle of inclination.
To approach the problem, first resolve the initial velocity into two components: horizontal and vertical. After that apply the equation of motion according to the given quantities. It will help to derive the angle of projection. Using that, find the range of projection using the formula of it.

Complete step by step answer:
In projectile motion, the motion along the two perpendicular axes is independent of each other. Therefore, in two-dimensional kinematics, the motion at a particular angle is resolved into two components, i.e. vertical and horizontal. The components of a projectile motion are as follows:
Time of Flight: It is defined as the time taken by the object to reach the surface once being projected. It depends on the initial velocity and the angle of inclination.
Maximum Height: In a projectile, maximum height is achieved when the vertical component of the velocity is zero. After attaining a maximum height, the object gets accelerated in the downward direction due to gravity.
Range: The maximum horizontal displacement covered by the projectile is known as range. The acceleration in the horizontal direction is zero as gravity only acts vertically.

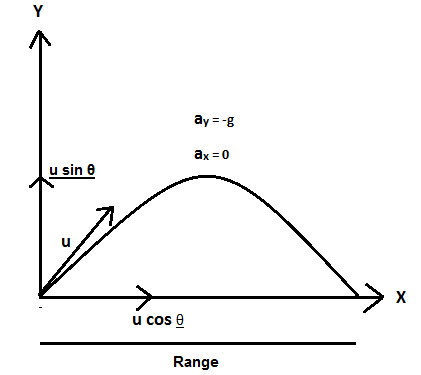
Now to solve the question, let’s assume that the body is projected at an angle, $\theta$ with an initial velocity of the body. Let the initial velocity be ‘$u$’. Now, resolve the initial velocity into two components: horizontal and vertical.
Horizontal component $= u\,\cos \theta$
Vertical component $= u\,\sin \theta$
Also, the acceleration along the X-axis is always zero and along the Y-axis, the acceleration is due to gravity represented by $g$. As the gravity acts in the downward direction, its sign is negative as shown in the figure. After $2s$ , it crosses a vertical distance, $s = 20cm$ .

So, the given quantities in the question are:
$u = 40m/s$
$g = - 9.8m/{s^2}$
$s = 20cm = 0.2m$
$t = 2s$
Using the second equation of motion along Y-axis we get:
$s = ut + \dfrac{1}{2}a{t^2}$
Along Y-axis the equation becomes:
$s = u\,\sin \theta \times t - \dfrac{1}{2}g{t^2}$
$\Rightarrow \,\,0.2 = 40\sin \theta \times 2 - \dfrac{1}{2} \times 9.8 \times {2^2}$
$\Rightarrow \,0.2 = 80\sin \theta - 19.6$
$\Rightarrow 80\sin \theta = 0.2 + 19.6$
$\Rightarrow \,\sin \theta = \dfrac{{19.8}}{{80}}$
So, the angle of inclination is:
$\sin \theta = \dfrac{{19.8}}{{80}}$
$\Rightarrow \sin \theta = 0.2475$
$\Rightarrow \,\theta = {\sin ^{ - 1}}(0.2475)$
$\Rightarrow \,\theta = 14.33^\circ$

The range of a projectile is given by:
$R = \dfrac{{{u^2}\sin 2\theta }}{g}$
$\Rightarrow R = \dfrac{{{{(40)}^2}\sin 2(14.33)}}{{9.8}}$
$\Rightarrow R = \dfrac{{1600 \times \sin (28.66)}}{{9.8}}$
$\Rightarrow R = \dfrac{{1600 \times 0.4796}}{{9.8}}$
$\therefore R = 78.3m$

Note: Gravity plays a crucial role in projectile motion. Once an object is projected with an initial force. After it gets projected, gravity is the only force that helps in the motion of the object in a parabolic curve.
If the angle of inclination is ${45^o}$ , then the object covers a maximum range. If the angle of inclination is ${90^o}$, then the object moves in a vertical direction, reaches a maximum height and then falls downwards due to gravity.