Solveeit Logo
Login

Question

Question: A body is projected up. At a point P in its path, the potential and kinetic energies of the body are...

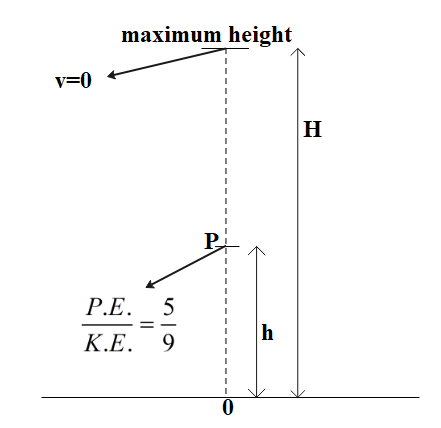
A body is projected up. At a point P in its path, the potential and kinetic energies of the body are in the ratio 5:95:9. The height of P and the maximum height to which the body can rise will be in the ratio
A.9:149:14
B.5:145:14
C.14:514:5
D.14:914:9

Explanation

Solution

We know that the energy of a system remains conserved at all times. In this problem, we shall take the body to be as our system and use conservation of its energy at two points, namely at point P and at the point of maximum height. We also know that the total energy of the body is equal to the sum of its kinetic and potential energy. Thus, we shall use the given ratios to substitute the values of energy and find the height P subsequently.

Complete answer:
The kinetic energy, K.E., of a body is given as:
K.E.=12mv2K.E.=\dfrac{1}{2}m{{v}^{2}}
Where,
m=m= mass of body
v=v= velocity of body
The gravitational potential energy, P.E., of a body is expressed as:
P.E.=mghP.E.=mgh
Where,
m=m= mass of body
g=g= acceleration due to gravity
h=h= height of the body
Let kinetic energy at point P be (K.E.)P{{\left( K.E. \right)}_{P}} and the potential energy at point P be (P.E.)P{{\left( P.E. \right)}_{P}}. It is given that the ratio of the two is 5:95:9.

⇒(P.E.)P(K.E.)P=59\Rightarrow \dfrac{{{\left( P.E. \right)}_{P}}}{{{\left( K.E. \right)}_{P}}}=\dfrac{5}{9}
⇒(P.E.)P=59(K.E.)P\Rightarrow {{\left( P.E. \right)}_{P}}=\dfrac{5}{9}{{\left( K.E. \right)}_{P}}
⇒(K.E.)P=95(P.E.)P\Rightarrow {{\left( K.E. \right)}_{P}}=\dfrac{9}{5}{{\left( P.E. \right)}_{P}} ………………. Equation (1)
Now, if the height at point P is hh, then (P.E.)P=mgh{{\left( P.E. \right)}_{P}}=mgh. ………………. Equation (2)
Let kinetic energy at maximum height, H be (K.E.)m{{\left( K.E. \right)}_{m}} and the potential energy at maximum height, H be (P.E.)m{{\left( P.E. \right)}_{m}}. When a body is projected upwards then at the highest point or the maximum height of its journey, its velocity becomes zero and thus its kinetic energy also becomes zero. At this point, the body only has potential energy (which is at its maximum value) due to the force of gravity acting on it.
⇒(K.E.)m=0\Rightarrow {{\left( K.E. \right)}_{m}}=0 and (P.E.)m=mgH{{\left( P.E. \right)}_{m}}=mgH …………………..Equation (3)
Conserving energy at maximum height and point P, we get
(K.E.)P+(P.E.)P=(K.E.)m+(P.E.)m{{\left( K.E. \right)}_{P}}+{{\left( P.E. \right)}_{P}}={{\left( K.E. \right)}_{m}}+{{\left( P.E. \right)}_{m}}
From equation (1), we get
⇒95(P.E.)P+(P.E.)P=(K.E.)m+(P.E.)m\Rightarrow \dfrac{9}{5}{{\left( P.E. \right)}_{P}}+{{\left( P.E. \right)}_{P}}={{\left( K.E. \right)}_{m}}+{{\left( P.E. \right)}_{m}}
⇒145(P.E.)P=(K.E.)m+(P.E.)m\Rightarrow \dfrac{14}{5}{{\left( P.E. \right)}_{P}}={{\left( K.E. \right)}_{m}}+{{\left( P.E. \right)}_{m}}
From equations (2) and (3), we get
⇒145(mgh)=0+(mgH)\Rightarrow \dfrac{14}{5}\left( mgh \right)=0+\left( mgH \right)
⇒145mgh=mgH\Rightarrow \dfrac{14}{5}mgh=mgH
Cancelling m and gm\text{ and }g from both sides, we get
⇒145h=H\Rightarrow \dfrac{14}{5}h=H
⇒hH=514\Rightarrow \dfrac{h}{H}=\dfrac{5}{14}
Therefore, the ratio of height of P and maximum height is 5:145:14.

Therefore, the correct option is (B) 5:145:14.

Note:
As the body starts falling down, it acquires both kinetic as well as potential energy because the body has now acquired some velocity. The lower the body falls down, the lesser is the height of the body. Thus, the potential energy decreases and kinetic energy increases as the body falls lower from its initial height.