Question

A body is projected horizontally from the top of an 80m height of a tower with certain velocity. If its equation of projectile is $80y={{x}^{2}}$ and $g=10m{{s}^{-2}}$. Then the angle made by its direction of motion with the horizontal after two seconds of motion is
A. $\dfrac{\pi }{2}$
B. $\dfrac{\pi }{3}$
C. $\dfrac{\pi }{4}$
D. $\dfrac{\pi }{6}$

Answer 1

As a first step compare the given equation of projectile with the standard equation. By rearranging, we get the horizontal initial velocity. Substituting this value of initial velocity in Newton’s equation of motion, find the horizontal displacement after 2s. Now you could differentiate the given equation with respect to x and then rearrange to get the slope. We know that tangent of the required angle gives us the slope of the trajectory and hence find the angle.
Formula used:
Equation of projectile,
$y=\tan \theta x-\dfrac{g{{x}^{2}}}{2{{\left( u\cos \theta \right)}^{2}}}$
Newton’s equation of motion,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete answer:
We are given the case of a horizontal projectile. A body is being projected from the top of an 80m building with some initial velocity (say, ${{u}_{x}}$). We are given the equation of projectile and also the value of acceleration due to gravity g. We are asked to find the angle made by its direction of motion with the horizontal after two seconds of motion.

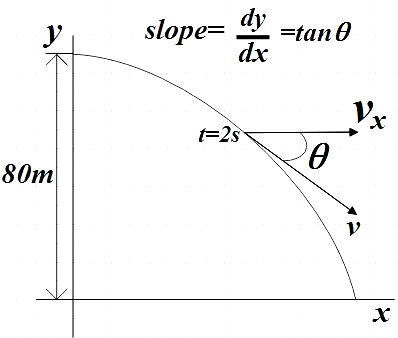
So, we are given the equation of the above horizontal projectile as,
$80y={{x}^{2}}$ …………………………….. (1)
We know that the standard equation of projectile is given by,
$y=\tan \theta x-\dfrac{g{{x}^{2}}}{2{{\left( u\cos \theta \right)}^{2}}}$ ………………………… (2)
For a body projected horizontally $\theta$ is zero. Therefore, (2) becomes,
$y=\dfrac{g{{x}^{2}}}{2{{u}^{2}}}$ ………………………………….. (3)
In equation (3) we have taken the acceleration as g not-g and hence negative sign in (2) is not there in (3).
Dividing (1) by (2) gives,
$\Rightarrow \dfrac{80y}{y}=\dfrac{{{x}^{2}}}{\dfrac{g{{x}^{2}}}{2{{u}^{2}}}}$
$\Rightarrow 80=\dfrac{2{{u}^{2}}}{g}$
$\Rightarrow u=\sqrt{\dfrac{80\times 10}{2}}=\sqrt{400}=20m{{s}^{-1}}$ ……………………………… (4)
We should note here that this velocity is the horizontal initial velocity, for a horizontal projectile the vertical initial velocity is zero.
From Newton’s equations of motion, we have,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
For a projectile motion, the horizontal motion is devoid of acceleration, so, the horizontal displacement after 2s is given by,
$\Rightarrow x=u\left( 2 \right)+0$
From (4),
$x=2\left( 20 \right)=40m$ ……………………………….. (5)
Differentiating (1) with respect to $x$ on both sides, we get,
$\Rightarrow 80\dfrac{dy}{dx}=2x$
$\Rightarrow \dfrac{dy}{dx}=\dfrac{2x}{80}$ ……………………….. (6)
We know that slope of the above trajectory is given by,
Slope = $\dfrac{dy}{dx}=\tan \theta$
From (6),
$\Rightarrow \tan \theta =\dfrac{2x}{80}$
From (5),
$\Rightarrow \tan \theta =\dfrac{2\times 40}{80}=1$
$\Rightarrow \theta ={{\tan }^{-1}}\left( 1 \right)=\dfrac{\pi }{4}$
Therefore, the angle made by the direction of motion of the body with the horizontal after two seconds of motion is $\dfrac{\pi }{4}$.

So, the correct answer is “Option C”.

Note:
While dealing with kinematics take care of the sign conventions used, for example, we have taken acceleration due to gravity as positive. You also have to know that $\theta$ in the equation of projectile is zero for horizontal projectile motion as it is the angle made by the body projected with the horizontal. Also, always remember that the tangent of the angle made by the direction of motion with horizontal gives you the slope of the trajectory.