Question

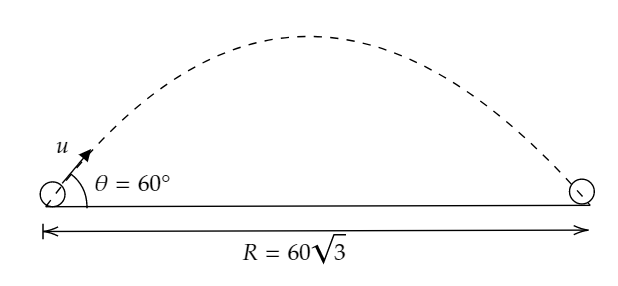
A body is projected from ground at angle ${60^ \circ }$ with the horizontal. If it comes back to the ground at distance $60\sqrt 3 {\text{ }}m$ from the starting point then what is the time of flight?

Answer 1

In this question, we have to find the initial value of velocity with the help of the formula to derive range, as the range of the projectile motion is given, Then by substituting the value of initial velocity that we got from the equation of range to the time of flight, we will find the answer.

Complete step by step solution:
It is given in the question that a body is projected from ground at angle ${60^ \circ }$ with the horizontal and it comes to the ground back at a distance $60\sqrt 3 {\text{ }}m$ from the starting point.
Hence, it is clear that the particle follows a projectile motion.

The formula to find the time of flight of projectile motion is given by,
$T = \dfrac{{2u\sin \theta }}{g} - - - - \left( 1 \right)$
The variables are defined as,
$T =$ Time of flight
$u =$ initial velocity of the particle
$\theta =$ angle of projection
$g =$ Acceleration due to gravity
In the given question, the range of the particle is given, $60\sqrt 3 {\text{ }}m$.
The formula for the range of a projectile motion is given as,
$R = \dfrac{{{u^2}\sin 2\theta }}{g} - - - - \left( 2 \right)$
The variables are defined as,
$R =$ range of the particle
$u =$ initial velocity of the particle
$\theta =$ angle of projection
$g =$ Acceleration due to gravity
Given in the question, $R = 60\sqrt 3 {\text{ }}m$, $g = 10{\text{ }}\dfrac{m}{{{s^2}}}$, $\theta = {60^ \circ }$.
Substituting the values in equation $\left( 2 \right)$ we get,
$60\sqrt 3 = \dfrac{{{u^2}\sin {{120}^ \circ }}}{{10}}$
$\Rightarrow 600\sqrt 3 = {u^2}\dfrac{{\sqrt 3 }}{2}$
Cross-multiplying we get,
$u = \sqrt {1200} = 20\sqrt 3$
Hence, the initial velocity of the particle is $20\sqrt 3 {\text{ }}\dfrac{m}{s}$.
Now by substituting all the values in equation $\left( 1 \right)$ we will find the time of flight,
$T = \dfrac{{2 \times 20\sqrt 3 \times \sin {{120}^ \circ }}}{{10}} = 6$
The time of flight is $6{\text{ }}s$.

Note:
It must be noted that the distance covered by the particle from the starting point is the range of the particle. In case of a projectile motion, the horizontal distance covered by a particle is defined as its range. The time of flight is considered to be the total time taken by a particle to reach the final point.