Question

A body is projected along a smooth inclined plane with a velocity $u$ From the point A as shown in the figure. The angle of inclination is ${45^ \circ }$ and the top is connected to a well of diameter $40{\text{ }}m$ . If the body just manages to cross the well, what is the value of $u$ . The length of the inclined plane is $20\sqrt 2 {\text{ }}m$ .

A. $40{\text{ }}m{s^{ - 1}}$
B. $40\sqrt 2 {\text{ }}m{s^{ - 1}}$
C. $20{\text{ }}m{s^{ - 1}}$
D. $20\sqrt 2 {\text{ }}m{s^{ - 1}}$

Answer 1

The body is located at a horizontal plane. As per the question the body projects from B and just crosses C, so it is a projectile motion and the distance between B and C is the range. Hence we will find the velocity from which it is projected from B. Then we have to find the acceleration at point B using a free body diagram and then find the initial velocity using Motion’s equation.

Complete step by step answer:

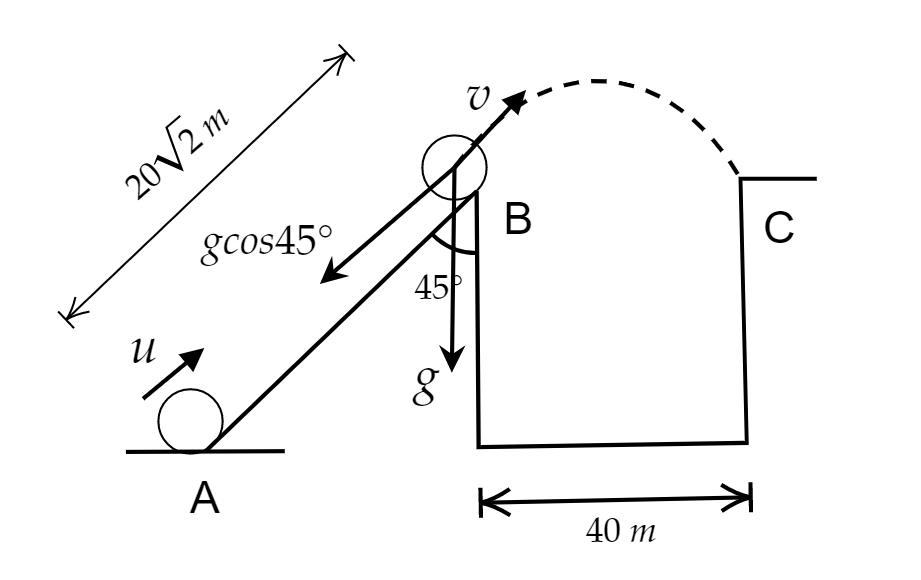
Let us consider that the velocity of the particle at which it projected from point B be $v$ .
As the particle just crosses the point C, hence its motion is projectile motion and the distance between B and C is the range of the particle.
The formula for the range of the particle is,
$R = \dfrac{{{v^2}\sin 2\theta }}{g}$
The variables are defined as-
$R =$ range of the particle
$v =$ velocity of the particle at which it is projected
$\theta =$ angle at which the body is projected with the horizontal
$g =$ acceleration due to gravity
The range of the particle $R = 40{\text{ }}m$
The angle of projection of the particle $\theta = {45^ \circ }$
Acceleration due to gravity $g = 10{\text{ }}\dfrac{m}{{{s^2}}}$
Substituting all the values we get,
$40 = \dfrac{{{v^2}\sin {{90}^ \circ }}}{{10}}$
$\Rightarrow v = 20$
The velocity at which the body is projected is $20{\text{ }}\dfrac{m}{s}$ .
Now, we have to find the initial velocity $u$ of the body.
The acceleration $a$ for the body is $g\cos {45^ \circ }$ .
By using the motion equation ${v^2} - {u^2} = 2as - - - \left( 1 \right)$ where, $v =$ final velocity, $u =$ initial velocity, $a =$ acceleration and $s =$ distance.
Here, $v = 20{\text{ }}\dfrac{m}{s}$ , $s =$ length of the inclined plane $= 20\sqrt 2 {\text{ }}m$ and $a = g\cos {45^ \circ } = \dfrac{{10}}{{\sqrt 2 }}{\text{ }}\dfrac{m}{{{s^2}}}$
Substituting the values in equation $\left( 1 \right)$ we get,
${\left( {20} \right)^2} - {u^2} = - 2 \times \dfrac{{10}}{{\sqrt 2 }} \times 20\sqrt 2$
$\Rightarrow - {u^2} = 800$
Square root of it gives,
$\therefore u = 20\sqrt 2 {\text{ }}m$
So, the correct option is D. $20\sqrt 2 {\text{ }}m{s^{ - 1}}$ .

Note:
It must be noted that the value of acceleration is given as negative, as it is acting in the opposite direction to which the velocity is applied. The range is the maximum distance which can be covered by a particle when it is projectile motion. As, the diameter of the well is the maximum distance which the body covers so it is considered to be the range.