Question

A body is moving down into a well through a rope passing over a fixed pulley of radius 10cm. Assume that there is no slipping between rope and pulley. Calculate the angular velocity and angular acceleration of the pulley at an instant when the body is going down at a speed of $20cm{{s}^{-1}}$ and has an acceleration of $4.0m{{s}^{-2}}$.

Answer 1

We know the linear velocity and the acceleration of the body. The radius of the rotating pulley is also known. From these we can directly find the angular velocity and angular acceleration of the pulley using the relations with the linear quantities.

Complete answer:
We are given the linear velocity and the linear acceleration of a body moving down on a rope hanging on a pulley. We know that the linear velocity and acceleration of the body is due to rotation of the pulley connected by the rope to the body. So, any linear motion of the body results in a consequent angular motion of the pulley or vice-versa.

                     ![](https://www.vedantu.com/question-sets/29c31e43-2f11-4108-b7af-de8db4e856a77829727261545712455.png)   

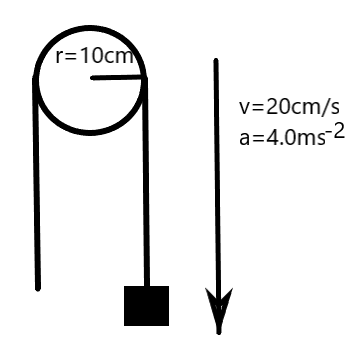
We know the relations connecting the linear quantities and the angular quantities. We can employ these relations in this situation to get the required solution.
The angular velocity and the linear velocity are related as –

& v=\omega .r \\\ & \Rightarrow \text{ }\omega =\dfrac{v}{r} \\\ \end{aligned}$$ The angular acceleration and the linear acceleration are related to each other as – $$\begin{aligned} & a=\alpha .r \\\ & \Rightarrow \text{ }\alpha =\dfrac{a}{r} \\\ \end{aligned}$$ Now, we can use these relations to find the required results of angular velocity and angular acceleration. The angular velocity is given by – $$\begin{aligned} & \omega =\dfrac{v}{r} \\\ & v=20cm/s, \\\ & r=10cm \\\ & \Rightarrow \text{ }\omega =\dfrac{20\times {{10}^{-2}}}{10\times {{10}^{-2}}}=2rad{{s}^{-1}} \\\ \end{aligned}$$ The angular acceleration is given as – $$\begin{aligned} & \alpha =\dfrac{a}{r} \\\ & a=4m{{s}^{-2}}, \\\ & r=10cm \\\ & \Rightarrow \text{ }\alpha =\dfrac{4}{10\times {{10}^{-2}}}=40rad{{s}^{-2}} \\\ \end{aligned}$$ The required solution is angular velocity is – $$\omega =2rad{{s}^{-1}}$$ And the angular acceleration is – $$\alpha =40rad{{s}^{-2}}$$ **Note:** The angular velocity and angular acceleration in this case is directly related to the linear velocity and linear acceleration. But, if the rope has a slipping with the pulley, then the linear and angular quantities will have frictional elements to be considered.