Question
Question: A body is lifted over route I and then over route II such that force is always tangent to the path. ...
A body is lifted over route I and then over route II such that force is always tangent to the path. Coefficient of friction is the same for both paths. Work done
(A). on both routes is same
(B). on route I is more
(C). on route II is more
(D). on both routes is zero
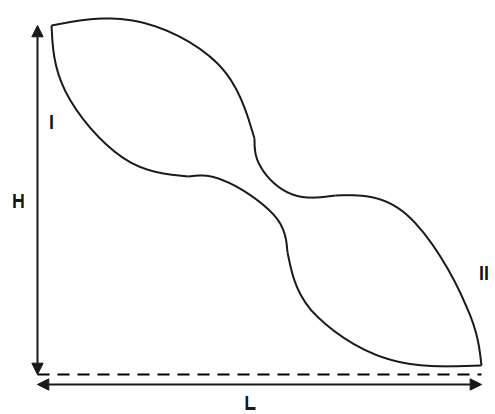
Solution
The figure shows two routes taken by a body such that force is always tangential to the path. Since the paths are almost identical to each other, their tangents will be parallel and the magnitude of force will be equal. Applying the work energy theorem, we can calculate the work done for both the paths.
Complete step by step answer:
Coefficient of friction is the ratio of the frictional force between two surfaces to the normal force acting between the surfaces. It is a unitless quantity. Therefore,
μ=NFr
Here, μ is the coefficient of friction
Fr is the frictional force
N is the normal force
The work done by a force is the product of force and displacement. Its SI unit is joules (J). Therefore,
W=Fx
Here, W is the work done
F is the force
x is the displacement
According to the work energy theorem, the difference between the work done to lift the body and the work done against friction is the total change in energy of a body. Therefore,
W=mgH+μmgL
Here, m is the mass of the body
g is the acceleration due to gravity
As the starting and the ending points for both the routes are the same and the coefficient of friction is also equal for both the routes. Therefore, from the above equation, the work done for both routes is the same.
So, the correct answer is “Option A”.
Note: The coefficient of friction is unitless because it is a ratio of the same units. According to work energy theorem sum of work done by all the forces on a particle is the change in energy of the particle. Work done on a body is conservative, i.e. it does not depend on the path but depends on the initial and final states.
