Question

A body is in limiting equilibrium on a rough inclined plane at angle ${{30}^{o}}$ with horizontal. Calculate the acceleration with which the body will slide down when the inclination of the plane is changed to ${{60}^{o}}$. (Take $g=10$m/$s^2$)

Answer 1

Draw the free body diagram to find the various forces acting on the body. Find the coefficient of friction from the limiting equilibrium condition. Utilise this in calculating the acceleration with which the body slides down.

Formula used: $a=\dfrac{{{F}_{n}}{{_{e}}_{t}}}{m}=\dfrac{mgsin\theta -\mu mgcos\theta }{m}$
$a$ is the acceleration of the body
${{F}_{n}}{{_{e}}_{t}}$ is the net force acting on the body
$m$ is the mass of the body
$g$ is the acceleration due to gravity
$\theta$ is the angle of inclination of the slope
$\mu$ is the coefficient of friction

Complete step by step solution:

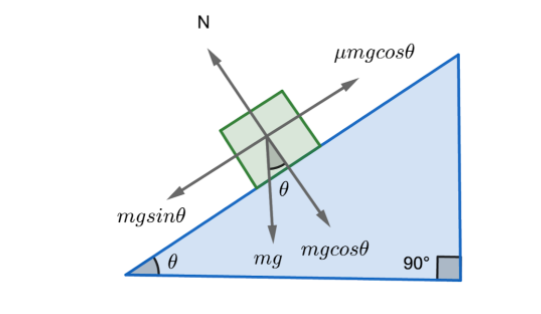
The forces acting on the body are:
1. Force of gravity
2. Normal force
3. Frictional force

The downward gravitational force is resolved into components, parallel and perpendicular to the surface. The normal force exerted by the incline on the object is given by $N$and is perpendicular to the incline surface. It exactly balances the component of gravitational force perpendicular to the surface such that $N=mg\cos \theta$. The frictional force experienced by the body is $f\le \mu N$ and is parallel to the incline surface. This frictional force prevents the object from sliding down the incline. In the limiting condition, it is at it’s maximum possible value.

In the first case when $\theta ={{30}^{o}}$, then the body is in limiting equilibrium such that ${{F}_{n}}{{_{e}}_{t}}=0$

& mg\sin \theta =\mu mgcos\theta \\\ & \mu =tan\theta \\\ & \mu =tan{{30}^{o}}=\dfrac{1}{\sqrt{3}} \\\ \end{aligned}$$ In the second case when $$\theta=60^o$$, then the body starts to slide down the incline. The acceleration is given by, $$\begin{aligned} & a=\dfrac{{{F}_{n}}{{_{e}}_{t}}}{m}=\dfrac{mgsin\theta -\mu mgcos\theta }{m} \\\ & a=g\sin {{60}^{o}}-\mu gcos{{60}^{o}}=\dfrac{10}{\sqrt{3}} m/s^2\\\ \end{aligned}$$ The body will slide down with acceleration $$a=\dfrac{10}{\sqrt{3}}$$m/$s^2$ when the inclination of the plane is increased. **Note:** The frictional force and normal force are contact forces whereas the gravitational force is non-contact force.