Question

A body is floating in water such that 6 out of 10 parts of its volume is underwater. Its density is
A) $0.6gm/cc$
B) $600kg/{m^3}$
C) both
D) none

Answer 1

A body in water or any fluid floats due to the buoyant force acting on the body. A body when is placed in a fluid it displaces some of the fluid and this gives rise to the buoyant force. You should apply the concept here as well.

Formula Used:
From Archimedes Principle, the buoyant force exerted by the fluid on a body fully or partially immersed in a fluid is equal to the weight of the fluid displaced by the body.
The buoyant force $F$ is defined as
$F = V{\rho _{fluid}}g$
where, ${\rho _{fluid}}$ is the density of the fluid the journey, $V$ is the displaced amount of fluid by the body and $g$ is the acceleration due to gravity.

Complete step by step solution:
Given:
The fluid is water.
The body has its $\dfrac{6}{{10}}$ of the total volume underwater.
We need to find the density of the body.
Step 1:
Let the density of the body is $\rho$ and the volume is $V$.
Hence, calculate the weight of the body.
$W = mg \\\ \Rightarrow W = \rho Vg \\\$
Step 2:
By the problem, the volume of the body underwater is $\dfrac{6}{{10}}V$.
The body will displace the equal volume of water as well.

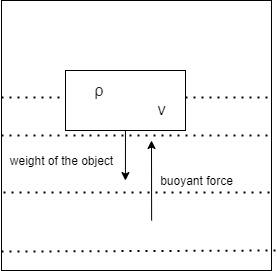
So, the volume of the displaced water ${V_w}$ is $\dfrac{6}{{10}}V$.
Hence this amount of water will contribute to the buoyant force.
The density of water is ${\rho _w} = 1g/cc = 1000kg/{m^3}$
Hence from eq (1), calculate the buoyant force $F$.
$F = {V_w}{\rho _w}g \\\ \Rightarrow F = \dfrac{6}{{10}}V{\rho _w}g \\\$
Step 3:
Now, the buoyant forces balance the weight of the body to keep it floating.
$\therefore W = F \\\ \Rightarrow V\rho g = \dfrac{6}{{10}}V{\rho _w}g \\\ \Rightarrow \rho = \dfrac{6}{{10}}{\rho _w} \\\$
Now for C.G.S unit,
$\rho = \dfrac{6}{{10}} \times 1gm/cc = 0.6gm/cc$
Now for SI unit,
$\rho = \dfrac{6}{{10}} \times 1000kg/{m^3} = 600kg/{m^3}$
$\therefore$ The density of the body is in the CGS unit $0.6gm/cc$ and in SI unit $600kg/{m^3}$.

A body is floating in water such that 6 out of 10 parts of its volume is underwater. Its density is both ($0.6gm/cc$ and $600kg/{m^3}$). Hence option (C) is correct.

Note:
The weight of the displaced water is equal to the weight of the whole body, not only the part immersed in water. You need to be carefully understood that the buoyant force completely balances the weight of the body and helps it float in a partially or fully immersed condition. You should carefully consider that option A and option B are in two different units so calculate the density of the body into different units as well.