Question

A body is executing circular motion in the vertical plane containing directions. If the direction of velocity $\vec{v}$ at the top most point is towards the west, what is the direction of angular velocity $\vec{\omega}$ ?
A. East
B. West
C. North
D. South

Answer 1

Sketch out the circular motion on the vertical plan and chart out the cardinal directions accordingly. Now, place your linear velocity vector at the top of the path traced by the body. Finding the direction of the angular velocity is now just a matter of using the right hand thumb rule. In other words, the angular velocity is always perpendicular to the linear velocity, so finding out the direction to which the $\vec{\omega}$ points to is now straightforward.

Complete answer:
We have a body undergoing circular motion in a vertical plane as shown in the figure.
$\vec{v}$ is the linear velocity of the body at the topmost point and is directed in the west direction.

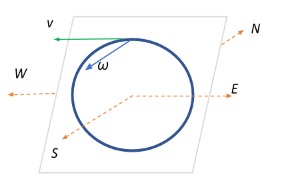
We are required to find the direction of the angular velocity. Let us consider the plane of motion having all the directions, as shown in the figure.
Angular velocity can be defined as a quantity that describes an object in circular motion, wherein its magnitude is equal to the linear velocity of the particle at that point, and its direction is perpendicular to the plane of motion.
To this end, we can deduce that the angular velocity vector $\vec{\omega}$ is directed either towards north or south. To further narrow it down, we will now consider the right hand rule.
According to the right hand rule, if you curl your fingers in the direction of circular motion of the body, the thumb then points in the direction of the angular velocity and subsequently the angular momentum vector as well.
Therefore, if we curl our right hand fingers towards the west, then our thumb points to the south, which is what we require.
Therefore, for the given setup, the angular velocity is directed perpendicular to the plane of motion and points towards the south.

So, the correct answer is “Option D”.

Note:
The reason why we find the angular versions of linear quantities such as velocity and momentum is because these quantities change as a body moves in a circle, as they are constantly subjected to a change in at least the direction at every point. Thus, the units of angular quantities are expressed per radian which measures the angular distance rather than per linear distance.

The relation between linear and angular velocity is $v =r\omega$, where r is the radius of the circular path traced by the body.