Question

A body is 1.8m tall and can see his image in a plane mirror fixed on a wall. His eyes are 1.6m from the floor level. The minimum length of the mirror to see his full image is.

A. 0.9m.
B. 0.85m.
C. 0.8m.
D. can’t be determined.

Answer 1

Firstly we will form a ray diagram which will give the basic idea to solve the question. After forming the ray diagram we will see two triangles visible $\vartriangle ECD\text{ and }\vartriangle EAB$. We will prove it similar and then using the property of similarity in triangles we will proceed further and obtain the answer.

Complete step by step answer:

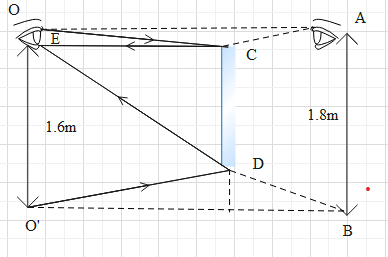
From the figure,
OO′ is the boy and point E represents the eyes of the boy.
Incident Ray OC is coming from the head of the boy and after getting reflected, ray CE enters the eye of the boy.
Incident Ray O′D is coming from the foot of the boy and after getting reflected, ray DE enters the eye of the boy.
The virtual image of the boy is drawn and is represented by AB.
Now,

& CD\parallel AB \\\ & \therefore \angle ECD=\angle EAB \\\ & \text{And }\angle EDC=\angle EBA \\\ \end{aligned}$$ So by AA similarity postulate we obtain $\begin{aligned} & \vartriangle ECD\sim \vartriangle EAB \\\ & =\dfrac{CD}{AB}=\dfrac{EC}{EA} \\\ \end{aligned}$ We know, $\dfrac{EC}{EA}=\dfrac{1}{2}$ Because the distance between image and the object is twice the distance between object and the mirror. $$\begin{aligned} & =\dfrac{CD}{AB}=\dfrac{1}{2} \\\ & \dfrac{CD}{1.8}=\dfrac{1}{2} \\\ & CD=0.9m \\\ \end{aligned}$$ **Note:** The first thing and very important thing to understand is that objects and their images on either side of a mirror are arranged in perfect symmetry. In-plane view, if one considers two eyes separated by a distance seeing a single image, it can be derived in a similar way that the horizontal length of the mirror required to see the full image of oneself is half the width of one's body at the widest point. We can see the object full image during a mirror half of an object height regardless of their distance from the mirror. The only thing is that the elevation of the top of the mirror should be exactly halfway between the level of eyes and the top of the head.