Question
Question: A body initially at rest, moves under the action of a constant force along a straight line. The inst...
A body initially at rest, moves under the action of a constant force along a straight line. The instantaneous power P developed by this force with time t is correctly represented by
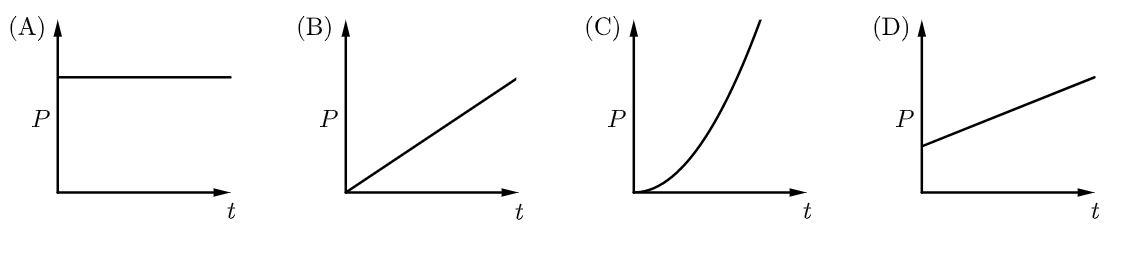
Solution
Hint The instantaneous power delivered by the force depends on the force and velocity of the body. And this force is proportional to acceleration of the body which is the velocity change per time.
Complete step-by-step solution :
Given the body has constant force and is moving along a straight line.
When the force is doing work actually it transfers one unit of energy. The rate of doing work is the same as the rate of doing energy.
The expression for instantaneous power delivered by the force is expressed by
P=OF.v=FvCosθ
Where, F is the force and v is the velocity and θ is the angle between the force and velocity.
Since the motion is in a straight line,
P=Fv
The expression for force according to Newton’s second law of motion is given as,
F=ma
Where, m is the mass and a is the acceleration.
Hence the force is constant, the acceleration will be also constant.
We know that velocity, v=at
This can be defined as v=kt hence the acceleration is a constant. And called as k .
Substitute this in the equation for power.
P=F×kt
Since F and k are constant, the power varies directly with time. Therefore the graph will be a straight line passing through the origin.
The answer is option B.
Note:- We have to note that if the two variables are proportional that varies in the same rate. Thus the graph will be a straight line which passes through the origin.
