Question
Question: A body initially at rest and sliding along a frictionless track from a height h(as shown in the figu...
A body initially at rest and sliding along a frictionless track from a height h(as shown in the figure) just completes a vertical circle of diameter AB=D. The height h is equal to.
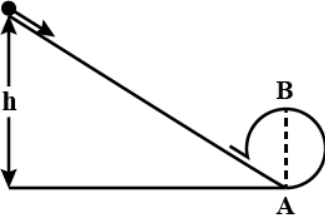
Solution
Hint : The mechanical energy formula states that mechanical energy is the sum of kinetic energy and the potential energy of the object.
Total Energy= K.E. + P.E.
Total Energy= 21mv2+mgh .
Complete Step By Step Answer:
As we know that the total initial energy of the body when it is in rest is equal to the potential energy. So,
Total energy at the start = mgh
Where
h is the initial height
g is gravity
m is the mass of the body
We also know that the total energy of the body at point B is the sum of kinetic and potential energy. So,
Total energy at point B= 21mv2+mgD
Where
m is the mass of the body
g is the gravity
D is the height of the body, since the body is circular in shape we will consider the diameter as the height.
v is the speed required for the rotation of the body, It is the minimum velocity required by the body to overcome the centripetal force while sliding down the hill top.
v=rg=2Dg
Since, radius( r )= 2D
Now,
Total Energy at start = Total Energy at point B
mgh=21mv2+mgD mgh=21m(2Dg)2+mgD mgh=21m2Dg+mgD mgh=41mgD+mgD mgh=45mgD h=45D
Hence, the initial height of the body is equal to five fourth of the diameter of the body.
Note :
The mechanical energy is conserved only when we ignore the external factors like air resistance, friction etc. If we include these factors then the mechanical energy is not equal to the sum of kinetic and potential energy.
