Question

A body covers first $\dfrac{1}{3}$part of its journey with a velocity of $2m/s$, next $\dfrac{1}{3}$ part with a velocity of $3m/s$and the rest of the velocity is $6m/s$. The average velocity of the body will be,
a. $3m/s$
b. $\dfrac{{11}}{3}m/s$
c. $\dfrac{8}{3}m/s$
d. $\dfrac{4}{3}m/s$

Answer 1

We can solve the given equation by finding the value of the average velocity of the body. We know the formula for the velocity that is displacement by time.

Formula used:
Velocity=$\dfrac{{{\text{displacement}}}}{{{\text{time}}}}$

Complete step by step answer:
We can consider the given values in the question. In the question it is given that the body covers first $\dfrac{1}{3}$ part of its journey with a velocity of $2m/s$, next $\dfrac{1}{3}$ part with a velocity of $3m/s$ and the rest of the velocity is $6m/s$.
Now we can draw a diagram with the given data.

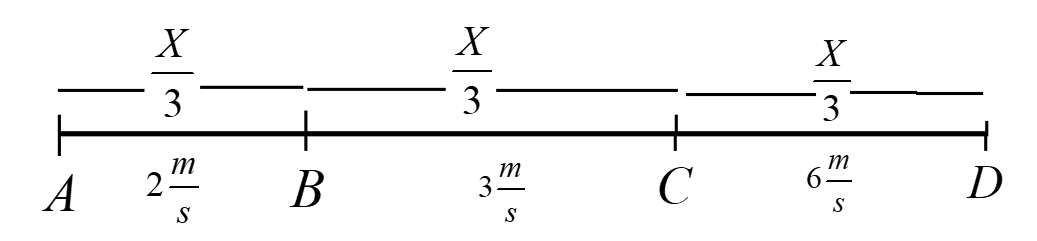
In the given diagram the values are mentioned. The velocities are $2m/s$, $3m/s$,$6m/s$. With the displacement of $\dfrac{X}{3}$.
We need to calculate the value of the average velocity. Velocity in physics is defined as the rate of change of the position of the object that is displaced with respect to the time of the reference frame. We need both the values of magnitude and the speed explains the velocity. In short, the velocity is the vector quantity. The meter per second $\left( {m/s} \right)$ is the S.I unit for the velocity. The velocity is the function of the displacement. The change in the velocity indicates that there is an acceleration acting on the object in a direction. The instantaneous velocity is the velocity of the time in a given moment and the average velocity can be calculated by dividing the total displacement and total time.
Now let us solve the given problem. We know the formula for the velocity. That is,
Velocity=$\dfrac{{{\text{displacement}}}}{{{\text{time}}}}$
To calculate the average velocity, we need to divide the total displacement and the total time taken. That is,
${V_{average}} = \dfrac{{T.D}}{{T.T}}$
Where, ${V_{average}}$ is the average velocity, $T.D$ is the total displacement and $T.T$ is the total time taken.
Time taken can be calculated as displacement by velocity. That is,
$\Rightarrow {t_1} = \dfrac{X}{{\dfrac{{\dfrac{x}{3}}}{2}}} \Rightarrow {t_1} = \dfrac{X}{{\dfrac{x}{6}}}$
$\Rightarrow {t_2} = \dfrac{X}{{\dfrac{{\dfrac{x}{3}}}{3}}} \Rightarrow {t_2} = \dfrac{X}{{\dfrac{x}{9}}}$
$\Rightarrow {t_3} = \dfrac{X}{{\dfrac{{\dfrac{x}{3}}}{6}}} \Rightarrow {t_3} = \dfrac{X}{{\dfrac{x}{{18}}}}$

By substituting the value of time in the equation we get,
$\Rightarrow {V_{average}} = \dfrac{{T.D}}{{T.T}}$
$\Rightarrow {V_{average}} = \dfrac{X}{{\dfrac{x}{6} + \dfrac{x}{9} + \dfrac{x}{{18}}}}$
On cancelling the $x$ terms we get,
$\Rightarrow {V_{average}} = \dfrac{1}{{\dfrac{1}{6} + \dfrac{1}{9} + \dfrac{1}{{18}}}}$
Taking L.C.M we get,
$\Rightarrow {V_{average}} = \dfrac{{18}}{{3 + 2 + 1}}$
$\therefore {V_{average}} = 3m/s$

Hence, the correct answer is option (A).

Note: The difference between the speed and the velocity must be known. Speed and velocity can be a little confusing, but note that speed gives the idea about how the object is moving. Whereas the velocity tells about the direction and the speed of the object.