Question

A body covered a distance of $L$ metres along a semi-circular path. Calculate the magnitude of displacement of the body and the ratio of distance to displacement.

Answer 1

A body moved along a semi-circular path between two points. The distance is the actual length covered by the body during its journey, but displacement is the shortest distance covered between its initial and final position. After getting distance and displacement, we will get the ratio of two terms.

Complete step-by-step solution:
Consider a body traveling along a semi-circular path. It moves from A to B.

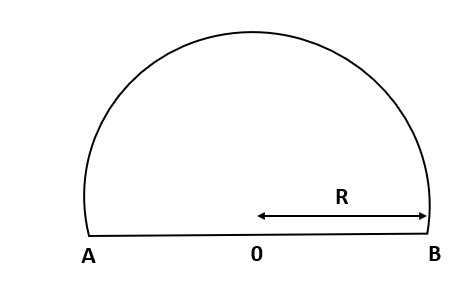
$L$ is the distance which is covered by the body.
$L$ is equal to half of the circumference of the circle.
$\therefore, L = \pi R$
So, the magnitude of the distance is $\pi R$.
Displacement is the shortest distance travelled by the object.
In this semicircle, the shortest distance between the two points A and B is the diameter of the semicircle.
Diameter is twice the radius.
$\therefore \text{displacement} = 2R$
So, the magnitude of the displacement is $2R$.
The ratio of distance to the displacement is:
$\dfrac{distance}{displacement} = \dfrac{\pi R}{2R}$
$\implies \dfrac{distance}{displacement} = \dfrac{\pi }{2}$
The ratio of distance to displacement is $\dfrac{\pi}{}2$.

Note: Displacement is the shortest length between any two locations when estimated along the minor path between them. To determine distance, the direction is not examined. To measure displacement, the direction is carried into consideration. Distance is a scalar measurement as it only depends upon the quantity and not the direction.