Question

A body B is capable of remaining stationary inside a liquid at the position shown in figure. If the whole system is gently placed on smooth inclined plane as shown in figure (b) and is allowed to slide down, then $\left( 0<\theta <90{}^\circ \right)$

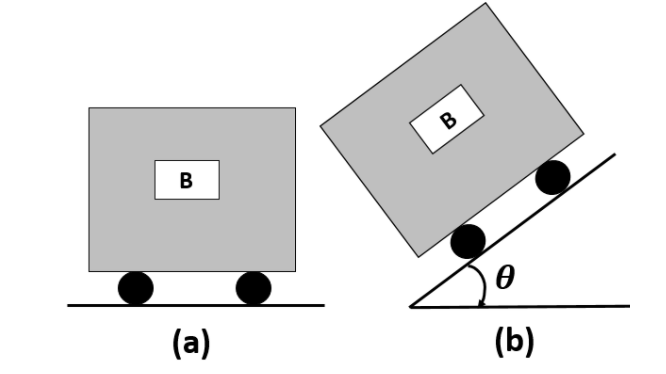
A. The body will move up (relative to the liquid).
B. The body will move down (relative to the liquid).
C. The body will remain stationary (relative to the liquid).
D. The body will move up for some inclination $\theta$ will move down for another inclination $\theta$.

Answer 1

To solve this question, we will consider the body as stationary (in equilibrium), which means that the weight of the body is balanced by the buoyant force, which is the law of floatation. Then, to find the condition of the body when placed on an inclined plane, we will need to resolve the weight of the body into components and then find the net acceleration down the plane.

Formula used: ${{F}_{B}}=w$
Where, ${{F}_{B}}$ is the buoyant force and w is the weight of the body.

Complete step by step answer:
We know that for a body to remain stationary in liquid, it must be in equilibrium condition. That means, its weight must be balanced with the upthrust/buoyant force provided by the liquid.
So, for the first case, where the body B remains stationary, we will have
${{F}_{B}}=w$

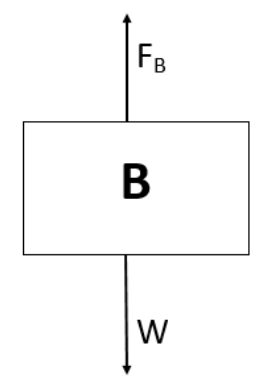
We must know that the buoyant force is given by the equation,
${{F}_{B}}={{\rho }_{l}}{{V}_{b}}g$
Where, ${{\rho }_{l}}$ is the density of the liquid.
${{V}_{l}}$ is the volume of the submerged body.
And g is the acceleration due to gravity.
And, weight of the body, w is given by,
$w={{\rho }_{b}}{{V}_{b}}g$
Where, ${{\rho }_{b}}$ is the density of the body.
${{V}_{b}}$ is the volume of the body.
And g is the acceleration due to gravity.

& \Rightarrow {{\rho }_{l}}{{V}_{b}}g={{\rho }_{b}}{{V}_{b}}g \\\ & \therefore {{\rho }_{l}}={{\rho }_{b}} \\\ \end{aligned}$$ Now, if the system is placed on an inclined plane, the weight of the body will be acting downwards which will be resolved to components.  So, here, the net buoyant force will be equal to, $${{F}_{B}}=w\sin \theta +w\cos \theta $$ So, if e look at some particular angles like ${{0}^{{}^\circ }},{{45}^{{}^\circ }}\text{and 9}{{0}^{{}^\circ }}$, ${{F}_{B}}=w$ That means the body B will remain at equilibrium at those angles. This will be carried out in all other angles inside $\left( 0<\theta <90{}^\circ \right)$. **So, the correct answer is “Option C”.** **Note:** We may be curious about why it will remain constant and the liquid will also be having a net force while placed at an inclined plane. But we must know that the buoyant force doesn’t depend on the acceleration affecting the liquid.