Question

A body at rest is acted upon by a constant force. What is the nature of the displacement-time graph?
A. Straight line
B. Symmetric parabola
C. Asymmetric parabola
D. Rectangular hyperbola

Answer 1

When a constant force is acting on a body it corresponds to constant acceleration. The nature of the displacement time curve can be determined using the equation of motion.

Complete answer:
A force due to which the body moves at a constant velocity with time and has constant non-zero acceleration is a constant force.
The force acting on a body of mass m is given by,
$F=ma$
$F\propto a$
If force is constant, acceleration will be constant.
To determine the nature of displacement time graph let us consider the equation of motion,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
$F\propto a$
Since the body is initially at rest $u=0$
And acceleration is constant
$\Rightarrow s=\dfrac{1}{2}a{{t}^{2}}$
$\Rightarrow s\propto {{t}^{2}}$
This equation is analogous to the equation of parabola i.e. $y=4a{{x}^{2}}$
Therefore, the displacement time graph is a parabola

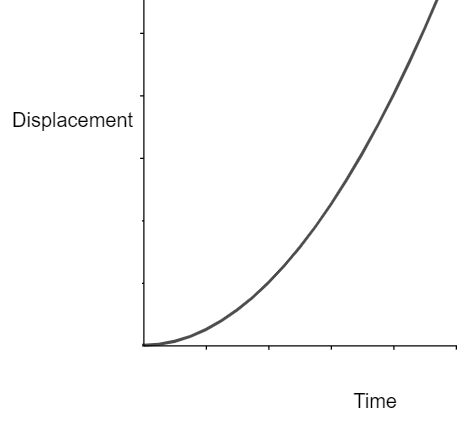
So, the correct answer is “Option B”.

Additional Information:
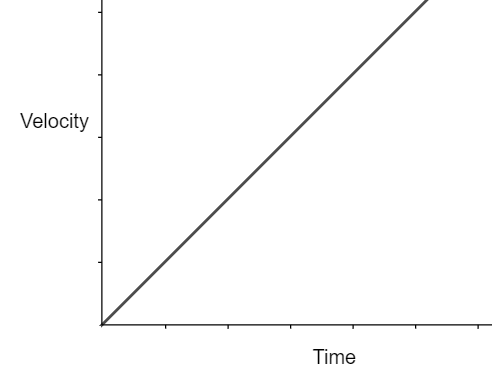
The nature of the velocity time graph would be a straight line if a constant force is applied. Using the first equation of motion i.e.
$v=u+at$
We get
$v\propto t$
Hence the velocity-time graph is a straight line.

An example of constant force is force of gravitation and the acceleration due to gravity is given by gravitational constant $g=9.8m{{s}^{-2}}$ for Earth.

Note:
Students should not confuse constant force with constant velocity. If the force acting on a body is constant it means it will have a constant non-zero acceleration and therefore an increasing velocity.