Question

A bob of mass m hangs from the ceiling of a smooth trolley car which is moving with a constant acceleration a. If the Young's modulus, radius and length of the string are Y, r and l respectively and if the stress in the string is $\dfrac{2m\sqrt{g^2+a^2}}{x\pi r^2}$ , find x.

Answer 1

Hint: We need to know the definition of stress. Then we will find the force on the bob along the string using Newton's third law of motion. Therefore, dividing this force by area, we can find the stress, and hence the answer.

Formula used:
$p=\dfrac{F}{A}$

Complete step-by-step solution:
There are two types of acceleration working on the bob. One is due to the gravity and the other is due to the acceleration of the moving trolley car. To find the acceleration due to the motion of the car, we will have to know about Newton's third law of motion. It states every force has an equal and opposite reaction. So, if the trolley moves in one direction, there will be another force acting on the bob in the opposite direction. The direction of all the accelerations are clearly depicted in the picture.

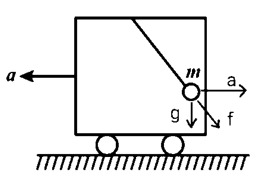
Now let f be the resultant acceleration. Since acceleration is a vector quantity, the magnitude of the resultant acceleration is given by,
$f=\sqrt{g^2+a^2}$
If ‘m’ the mass of the bob, the total force on the bulb is given as,
$F=mf$
Now stress is defined as the force per unit area. The cross-sectional area of the string is $\pi r^2$. So, the stress on the string is giving as,
$p=\dfrac{F}{A}=\dfrac{m\sqrt{g^2+a^2}}{\pi r^2}$
Now, we have to equal this expression with the expression given in the question. Then we easily get, $x=2$. It is the final answer.
Additional information:
Stress is dimensionally the same as pressure. The only difference is that, pressure is the external force per unit area and stress is the force that is generated within the string per unit area.

Note: Stress is not any force per unit area, but the force that is normal to the cross section of the string. Don’t take the acceleration a of the bob along the direction of motion of the trolley. It’s just the opposite. The Young's modulus and the length of the string is not necessary to solve this problem.