Question

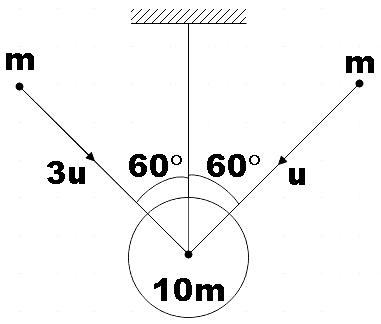
A bob of mass $10m$ is suspended through an inextensible string of length l. When the bob is at rest in equilibrium position, two particles each of mass m strike it as shown in the figure. The particles stick after collision. Choose the correct statement from the following.
A. Impulse in the string due to tension is 2mu.
B. Velocity of the system just after collision is $v=\dfrac{u\sqrt{3}}{14}$
C. Loss of energy is $\dfrac{137}{28}m{{u}^{2}}$
D. Loss of energy is $\dfrac{137}{56}m{{u}^{2}}$

Answer 1

You may recall that the impulse by definition is the change in momentum and the impulse in the string due to tension will be the change in momentum along the vertical direction. For finding the velocity after collision, you’d use the law of conservation of linear momentum. Also, loss of energy will be the change in initial and final energy.

Complete Step by step solution:
In the question, we are given a bob of mass 10m that is suspended on a string of l length. Two particles of mass m strikes when the bob is in the equilibrium position and they stick to the 10m bob after this collision. We are asked to find the correct statement from the given statements above.

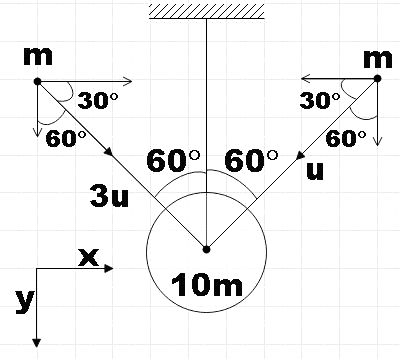
We know that impulse by definition is the change in momentum. So the impulse in the string due to tension will be the change in momentum in the vertical direction. As the string is inextensible, there will be no momentum in the vertical direction after collision. So, the change in momentum along y-direction for the system will be the sum of change in momentum of the particles in the y-direction,
$I=\Delta P=\left( 3mu\cos 60{}^\circ -0 \right)+\left( mu\cos 60{}^\circ -0 \right)$
$\Rightarrow I=\dfrac{mu}{2}\left( 3+1 \right)$
$\therefore I=2mu$
So, statement A is found to be correct.

Let us apply conservation of linear momentum along the x-direction,
$3mu\sin 60{}^\circ -mu\sin 60{}^\circ =\left( 10m+m+m \right)V$
$\Rightarrow 12mV=\dfrac{\sqrt{3}mu}{2}\left( 3-1 \right)$
$\therefore V=\dfrac{\sqrt{3}u}{12}$
So, we found the velocity after collision to be $V=\dfrac{\sqrt{3}u}{12}$.
Hence, statement B is false.

The loss of energy will be given by the difference of its initial and final energies.
$\left( \dfrac{1}{2}m{{\left( 3u \right)}^{2}}+\dfrac{1}{2}m{{u}^{2}} \right)-\dfrac{1}{2}\left( 12m \right){{V}^{2}}=L.E$
$\Rightarrow L.E=\dfrac{1}{2}m{{u}^{2}}\left( 9+1-\dfrac{3}{12} \right)$
$\therefore L.E=\dfrac{39}{8}m{{u}^{2}}$
Therefore, we found that both statements C as well as D are wrong.

Hence, we found that option A is the correct answer.

Note:
In questions that involve finding the true statement, there is a possibility for multiple options being correct. So, we have to check whether other options are correct even if we find the very first option to be the correct statement. Here, however only one statement is correct.