Question

A bob is projected with speed of $\sqrt {3gL}$ from the bottommost point of vertical circular motion. Find angle $'\theta '$ with vertical at which bob leaves circular motion. If $'L'$ is the length of the string.

Answer 1

In vertical circular motion, object tends to complete a circular motion in vertical plane, we will use the concept of Law of conservation of energy which can be stated as change in kinetic energy from point A to point B is equals to the gravitational potential energy if object is raised to some height.

Complete step by step answer:
Let us suppose bob is projected at point A with a velocity of $\sqrt {3gL}$ and when it reaches the point B let its velocity be ${V_b}$ and at point B bob leaves the circular motion when it makes an angle of $\theta$ with the vertical axes as shown in the diagram.

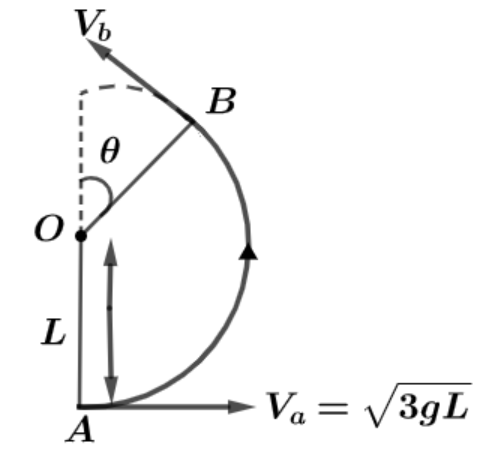
Total height from point A to point B can be written as $L + L\cos \theta$
Gravitational potential energy up to this point is $- mg(L + L\cos \theta )$
Kinetic energy of bob at point A can be written as $\dfrac{1}{2}m{V_a}^2$
$K.{E_A} = \dfrac{1}{2}m(3gL)$
Kinetic energy at point B can be written as $\dfrac{1}{2}m{V_b}^2$
$K.{E_B} = \dfrac{1}{2}m{v_b}^2$
Now, from law of conservation of energy, the difference of kinetic energy between points from B to point A is equals to the gravitational potential energy, so we can write as
$\dfrac{1}{2}m{v_b}^2 - \dfrac{1}{2}m(3gL) = - mg(L + L\cos \theta )$
Or
${v_b}^2 - (3gL) = - 2Lg(1 + \cos \theta )$
Or
${v_b}^2 = Lg(1 - 2\cos \theta ) \to (1)$
Now, since at point B just when bob leaves circular motion and balanced by force of gravity which can be written as:
$\dfrac{{m{v_b}^2}}{L} = mg\cos \theta$
Or
${v_b}^2 = Lg\cos \theta \to (2)$
So from equation $(1)and(2)$ we get,
$gL-2gl\cos \theta = gL\cos \theta$
Or
$\cos \theta = \dfrac{1}{3}$
Or
$\theta = {\cos ^{ - 1}}(\dfrac{1}{3})$
Hence, the angle with the vertical made by bob is $\theta = {\cos ^{ - 1}}(\dfrac{1}{3})$ .

Note: It should be remembered that, force acting on a body while moving in circular motion is called centripetal force and its magnitude is governed by the formula ${F_c} = \dfrac{{m{v^2}}}{r}$ which acts towards the centre of the circular path and in circular motion the direction of the velocity of a body at any point on the circular path is towards the direction of tangent at that point.