Question
Question: A bob hangs from a rigid support by an inextensible string of length \[l\] (from the lowest position...
A bob hangs from a rigid support by an inextensible string of length l (from the lowest position) keeping the string straight, and then released. The speed of the bob at the lowest position is
A.gl
B.3gl
C.2gl
D.5gl
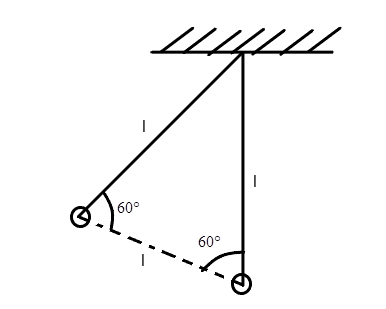
Solution
Hint : We need to use the principle of conservation of energy between the highest point and the lowest point. For calculation of potential energy, find the vertical distance of the bob at the highest position from the lowest position.
Formula used:
In this solution we will be using the following formulae;
PE=mgh where PE is the potential energy of a body from a reference point, m is the mass of that body, g is the acceleration due to gravity and h is the vertical height of the body from the reference point.
KE=21mv2 where KE is the kinetic energy of the body, and v is the velocity of the body.
Complete answer:
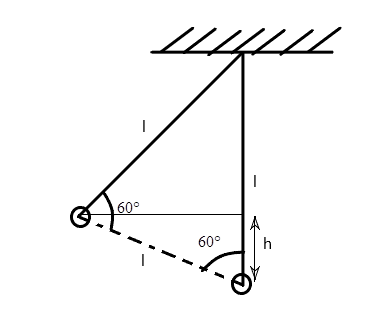
First, we see from diagram, that the height of the bob above the lowest point can be given by
h=lcos60=2l
Now, using the lowest point as the reference point, the potential energy of the bob can be found using the formula
PE=mgh where m is the mass of that body, g is the acceleration due to gravity and h is the vertical height of the body from the reference point.
Hence,
PE=mg2l
Now, according to the principle of conservation of energy, all the potential at the highest point will be converted to kinetic energy at the lowest point. The kinetic energy is
KE=21mv2 where v is the velocity of the body.
Hence,
mg2l=21mv2
Hence, by making v subject of the formula, we have
v=gl
Hence, the correct option is A.
Note:
For clarity, note that the point of reference is not essential to the calculation of the velocity, any point can be used as a reference point. The potential energy is always based on some point of reference.
