Question

A boat travels from the south bank to the north bank of a river with a maximum speed of $8km/h$. A river current flows from west to east with a speed of $4km/h$. Find the angle with which the boat should be steered to arrive at a point opposite to the point of start.
(a) ${60^\circ }W\,of\,N$
(b) ${30^\circ }W\,of\,N$
(c) ${60^\circ }S\,of\,E$
(d) ${30^\circ }S\,of\,E$

Answer 1

In order to answer this question, we have to calculate the angle with which the boat should be steered to arrive at a point opposite to the point of start, we will first draw a diagram respect to the given problem and then we will take sine angle to solve for it.

Complete step by step answer:
Velocity of the boat $= 8km/h$
And, the velocity of the river from west to east $= 4km/h$
So, according to the question:

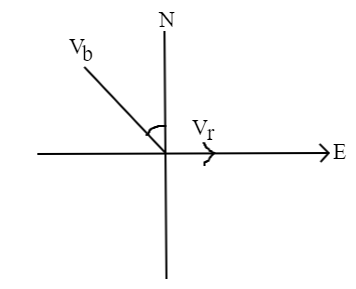
In the above figure, the angle is $\theta$ .
So, as the angle with which the boat should be steered to arrive at a point opposite to the point of start is as:
${V_{br}}\sin \theta = v \\\ \Rightarrow \sin \theta = \dfrac{4}{8} = \dfrac{1}{2} \\\$
$\therefore \theta = {30^\circ }\,west\,of\,north$ .
Therefore, the angle with which the boat should be steered to arrive at a point opposite to the point of start is ${30^\circ }W\,of\,N$ .
Hence, the correct option is (b).

Note: As we know, the given question is related to the river boat topic, so to solve river boat problems, we need to understand two concepts: The speed of a boat relative to the water is equal to the speed of the boat in still water.