Question

A boat takes 2 hours to travel 8 km and back in a still water lake. With water velocity of 4Km/hr , the time taken for going upstream 8 km and coming back is:
A.160 minutes
B.80 minutes
C.100 minutes
D.120 minutes

Answer 1

In order to solve this question first by the help of given statement we will first calculate the speed of boat in still water and then with the help of speed of stream or velocity of water we will calculate the velocity in upstream direction and downstream direction and then with the help of upstream and downstream speed we will find the time taken.

Complete answer:
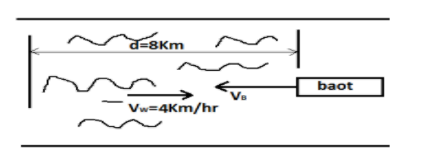
The diagram below is showing the scenario when the speed of the water is not zero, that means when the speed of the water velocity $4$Km/hr.

Formula used: $speed = \dfrac{{distance}}{{time}}$
Given that:
Boat takes two hours to fly 8 km in a still water lake.
So the total distance will be $8Km + 8Km = 16Km$
Time taken = 2 hours
As we know the relation between distance, speed and time is:
$speed = \dfrac{{distance}}{{time}}$
So, the speed of boat in still water = total distance / total time
Speed of the boat= ${V_B}$= $\dfrac{{16Km}}{{2hr}}$
$\Rightarrow {V_B} = 8$Km/hr
It is given that the water velocity is 4Km/hr.
Now if we observe the diagram for the downstream,
Velocity in downstream direction =(Speed of boat in still water-Water velocity)
=8km/hr + 4km/hr =12 Km/hr
Time for traveling 8km downstream =
$time{\text{ }}taken{\text{ }}by{\text{ }}the{\text{ }}boat = {t_B} = \dfrac{{distance{\text{ }}covered}}{{speed{\text{ }}of{\text{ }}the{\text{ }}boat}}$
$\Rightarrow {t_B} = \dfrac{8}{{12}}hr$
$\Rightarrow {t_B} = \dfrac{2}{3}hr$
Now according to the situation in the diagram,m,
The velocity in upstream direction = (Speed of boat in still water - Water velocity)
= (8-4)Km/hr = 4Km/hr
Time for traveling 8km upstream =
$time{\text{ }}taken{\text{ }}by{\text{ }}the{\text{ }}boat = {t_B} = \dfrac{{distance{\text{ }}covered}}{{speed{\text{ }}of{\text{ }}the{\text{ }}boat}}$
$\Rightarrow {t_B} = \dfrac{8}{4}hr$
$\Rightarrow {t_B} = 2hr$
Total time for traveling = (Time for traveling 8km downstream + Time for traveling 8km upstream)
$= \dfrac{2}{3}hr + 2hr$
$= \dfrac{8}{3}hr$
$= \dfrac{8}{3}hr \times 60\min$
$= 160\min$
Hence, the time taken for going upstream 8 km and coming back is 160 min

So, the correct answer is option (A).

Note:
Downstream direction is the direction of the stream, which is called upstream direction toward the stream. Students need to consider the relationship between speed, distance and time, as it is one of the most important mechanical relationships. Also students must remember the speed of the boat upstream and downstream in terms of stream speed.