Question

A boat of mass $80Kg$ is floating on still water. A dog of mass $20Kg$ on the boat at a distance of $10m$ from the shore. The dog moves on the boat by a distance of $2m$ towards the shore. The distance of the dog from the shore will be given by,
$\begin{aligned} & A.11.6m \\\ & B.8.4m \\\ & C.9.6m \\\ & D.10.4m \\\ \end{aligned}$

Answer 1

First of all draw a diagram for a clear understanding of the question. The resultant distance of the dog from the shore is found by taking the difference between the distance of the boat from the shore and the distance by which the centre of mass of the whole system moves when the dog on boat is moved by a distance of $2m$. So first of all let us find out the movement in position of centre of mass of the system. These all may help you to solve this question.

Complete answer:

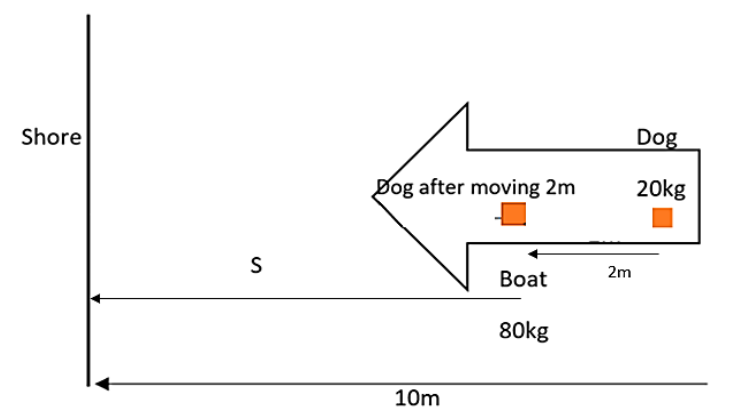
First of all let us mention the values given in the question.
Mass of the boat is given as,
$M=80Kg$
Mass of the dog is given as,
$S=10-1.6=8.4m$
The distance of the boat from the shore has been mentioned as,
$d=10m$
The distance by which the dog in the boat moves towards the shore is given as,
$l=2m$
As we mentioned the dog is moving towards the shore by sitting inside the boat. Therefore the centre of mass of the system including the boat and the dog has moved a distance $2m$. So first of all let us calculate the shift in centre of mass,
$X=\dfrac{Ml}{M+m}$
Substituting the values in it will give,
$X=\dfrac{80\times 2}{80+20}=\dfrac{160}{100}=1.6m$
This is the shift in centre of mass. Now the resultant distance of the dog from the shore can be found by taking the difference between the $d$ and $X$.
Therefore we can write that,
$S=d-X$
Substituting the values in the equation,
$S=10-1.6=8.4m$

Therefore the correct answer is option B.

Note:
Shift in the centre of mass is given as, if some mass of a body is moved, the centre of mass moves towards the heavier mass. It tells that the moments of a system in one direction are equivalent in magnitude and opposite in direction to the moments of the similar system in the reverse direction.