Question

A boat of mass 40kg is floating on water. A boy of mass 10kg on the boat moves by 8m towards the shore. The distance by which the boat moves away from the shore is
A. 4m
B. 3m
C. 2m
D. 1.6m

Answer 1

As we can see, there are no external force acts on the boat. Therefore, the centre of mass of the system does not change. Recall the formula for centre of mass. Determine the displacement of the boy with respect to the shore.

Formula used:
Centre of mass, ${r_{cm}} = \dfrac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}}$
Here, ${m_1}$ is the mass of the first particle, ${m_2}$ is the mass of the second particle, ${r_1}$ is the position of the first particle and ${r_2}$ is the position of the second particle.

Complete step by step answer:
Let the mass of boy is ${m_1} = 10\,{\text{kg}}$, the mass of boat is ${m_2} = 40\,{\text{kg}}$ and the distance moved by the boat away from the shore is x.As we can see, there is no external force acts on the boat. Therefore, the centre of mass of the system does not change. To keep the centre of mass of the system the constant, $\Delta {r_{CM}}$ should be zero.We have the expression for the centre of mass,
$\Delta {r_{CM}} = \dfrac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}} = 0$
$\Rightarrow {m_1}{r_1} + {m_2}{r_2} = 0$
$\Rightarrow {m_1}{r_1} = - {m_2}{r_2}$
Here, ${r_1}$ is the displacement of the boy and ${r_2}$ is the displacement of the boat.

Let us observe the following figure,

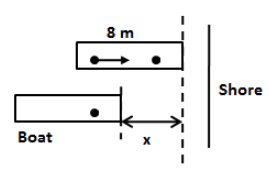
From the above figure, the displacement of the boy with respect to the shore is $\left( {8 - x} \right)\,{\text{m}}$ and the displacement of the boat is $- x\,{\text{m}}$. Substituting $\left( {8 - x} \right)\,{\text{m}}$ for ${r_1}$ and $- x\,{\text{m}}$ for ${r_2}$ in the above equation, we get,
${m_1}\left( {8 - x} \right) = - {m_2}\left( { - x} \right)$
$\Rightarrow 8{m_1} - {m_1}x = {m_2}x$
$\Rightarrow x = \dfrac{{8{m_1}}}{{{m_1} + {m_2}}}$
Substituting ${m_1} = 10\,{\text{kg}}$ and ${m_2} = 40\,{\text{kg}}$ in the above equation, we get,
$x = \dfrac{{8\left( {10} \right)}}{{10 + 40}}$
$\Rightarrow x = \dfrac{{80}}{{50}}$
$\therefore x = 1.6\,{\text{m}}$
Thus, the distance moved by the boat with respect to the shore is 1.6 meter.

So, the correct answer is option D.

Note: Students must note that when the external force acting on the system is zero, the centre of mass of the system does not change. In the solution, we have taken the change in centre of mass and therefore, we have taken the displacement of the boy and boat rather than position of the boy and boat. The displacement of the boat is with respect to the shore and not from the shore.