Question

A boat moves with a speed of $5\,{\text{km/h}}$ relative to water in a river flowing with a speed of $3\,{\text{km/h}}$ and having a width of $1\,{\text{km}}$. The minimum time take around a round trip is:
A. $5\,{\text{min}}$
B. $60\,{\text{min}}$
C. $20\,{\text{min}}$
D. $30\,{\text{min}}$

Answer 1

Determine the speed of the boat required to complete one round trip in minimum time which is perpendicular to the river flow. Use the formula for speed of an object to determine the time required for the boat to reach the other edge of the river. Multiply this time by 2 to determine the minimum time for one round trip of the boat.

Formula used:
The speed $v$ of an object is given by
$v = \dfrac{d}{t}$ …… (1)
Here, $d$ is distance travelled by the object and $t$ is the time required to travel the same distance.

Complete step by step answer:
We have given that the speed of the boat relative to water is $5\,{\text{km/h}}$.
${v_{BW}} = 5\,{\text{km/h}}$
The speed of the water flowing in the river is $3\,{\text{km/h}}$.
${v_w} = 3\,{\text{km/h}}$
The width of the river is $1\,{\text{km}}$.
$W = 1\,{\text{km}}$
We have asked to determine the minimum time required for one round trip of the boat.The time required for the boat to complete one round trip will be minimum if it is travelled in a direction perpendicular to the flow of water in the river. Let us draw the diagram for the velocities of the boat and water.

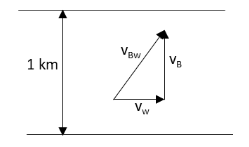
In the above diagram, ${v_B}$ is the speed of the boat. Let us determine the speed of the boat in the perpendicular direction to the flow of water in the river.
$v_w^2 + v_B^2 = v_{Bw}^2$
Substitute $3\,{\text{km/h}}$ for ${v_w}$ and $5\,{\text{km/h}}$ for ${v_{Bw}}$ in the above equation.
${\left( {3\,{\text{km/h}}} \right)^2} + v_B^2 = {\left( {5\,{\text{km/h}}} \right)^2}$
$\Rightarrow v_B^2 = 25 - 9$
$\Rightarrow v_B^2 = 16$
$\Rightarrow {v_B} = 4\,{\text{km/h}}$
Hence, the speed of the boat in perpendicular direction is $4\,{\text{km/h}}$.

Now let us determine the time required for the boat to reach the other edge of the river.
Rewrite equation (1) for the speed of the boat.
${v_B} = \dfrac{W}{t}$
$\Rightarrow t = \dfrac{W}{{{v_B}}}$
Substitute $1\,{\text{km}}$ for $W$ and $4\,{\text{km/h}}$ for ${v_B}$ in the above equation.
$\Rightarrow t = \dfrac{{1\,{\text{km}}}}{{4\,{\text{km/h}}}}$
$\Rightarrow t = 0.25\,{\text{h}}$

The time $T$ required for one round trip is twice the time $t$ required for the boat to reach the other edge of the river.
$T = 2t$
Substitute $0.25\,{\text{h}}$ for $t$ in the above equation.
$T = 2\left( {0.25\,{\text{h}}} \right)$
$\Rightarrow T = 0.5\,{\text{h}}$
$\Rightarrow T = \left( {0.5\,{\text{h}}} \right)\left( {\dfrac{{60\,{\text{min}}}}{{1\,{\text{h}}}}} \right)$
$\therefore T = 30\,{\text{min}}$
Therefore, the time required for the boat for one round trip is $30\,{\text{min}}$.

Hence, the correct option is D.

Note: The students should not forget to determine the speed of boat perpendicular to flow of the river because the given speed of the boat relative to water will not give the minimum time required for the boat to complete one round trip in the river. Also, the students should not forget to multiply the determined time by 2.