Question

: A boat moves relative to water with velocity $v$ , and the river is flowing with$2v$. At what angle the boat shall move with the stream to have minimum drift?
A. ${30^ \circ }$
B. ${60^ \circ }$
C. ${90^ \circ }$
D. ${120^ \circ }$

Answer 1

In this question, we need to determine the angle at which the boat should move with the stream with the minimum drift to reach the opposite bank of the river. For this, we will use the concept of relative velocity which is the velocity of an object with respect to another object.

Complete step by step answer:
Let the relative velocity of the boat is ${u_b} = v$
The velocity of the river is ${u_r} = 2v$in the horizontal direction
Now let the angle be $\theta$made by boat to have minimum drift

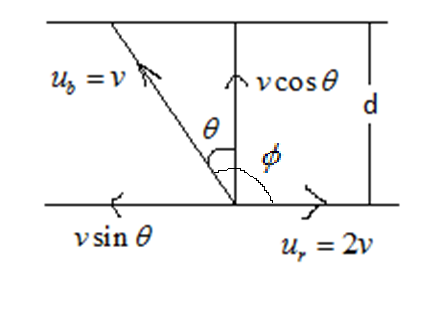
Hence we can write the horizontal and vertical component of velocity of the boat as
${v_x} = 2v - v\sin \theta - - (i)$
${v_y} = v\cos \theta - - (ii)$
Let the width of the river be ‘d’.
So the time required to cross the river will be
$t = \dfrac{d}{{\cos \theta }} - - (iii)$[Since$time = \dfrac{{dis\tan ce}}{{speed}}$]
Since we have observed that${v_x} > 0$, so we can say drift is not equal to 0.
As we know, drift is$X = {v_x} \times t$, hence by solving, we get

$$X = {v_x} \times t \\\ = \left( {2v - v\sin \theta } \right) \times \dfrac{d}{{v\cos \theta }} - - (iv) \\\$$

Now for x to be minimum, let’s differentiate equation (iv) w.r.t $\theta$

$$\dfrac{{dX}}{{d\theta }} = 0 \\\ \dfrac{{d\left[ {\left( {2v - v\sin \theta } \right) \times \dfrac{d}{{v\cos \theta }}} \right]}}{{d\theta }} = 0 \\\ \dfrac{d}{{d\theta }}\left[ {\dfrac{{2vd}}{{v\cos \theta }}} \right] - \dfrac{d}{{d\theta }}\left[ {\dfrac{{d \times v\sin \theta }}{{v\cos \theta }}} \right] = 0 \\\ d\left( {2\dfrac{d}{{d\theta }}\left[ {\sec \theta } \right] - \dfrac{d}{{d\theta }}\left[ {\tan \theta } \right]} \right) = 0 \\\ d\left[ {2\sec \theta \tan \theta - {{\sec }^2}\theta } \right] = 0 \\\ 2\sec \theta \tan \theta - {\sec ^2}\theta = 0 \\\$$

By further solving this equation, we get

$$2\sec \theta \tan \theta = {\sec ^2}\theta \\\ 2\tan \theta = \sec \theta \\\ 2\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{{\cos \theta }} \\\ \sin \theta = \dfrac{1}{2} \\\$$

So the values of the angle $\theta$will be

$$\theta = {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) \\\ = {30^ \circ } \\\$$

This angle is made with the vertical so, to make the angle with the horizontal axis, add 90 degrees with the 30 degrees to get the result.
Hence, the angle at which the boat shall move with the stream to have minimum drift
$\theta + \phi = {90^ \circ } + {30^ \circ } = {120^ \circ }$
Option D is correct.

Note: It is worth noting down here that, the boat can also move with other angles also, but to satisfy the need to the question that there should be minimum drift to reach at directly opposite bank of the river we need to move the boat at an angle of 120 degrees with the horizontal.