Question

A boat moves relative to water with a velocity which is n=2.0 times less than the river flow velocity. The angle (in degrees) to stream direction must the boat move to minimize drifting is $(120+x)$. The value of $x$ is

Answer 1

To solve this type of question we use the concept of drift velocity.velocity is defined as the distance covered per unit time. For river flow, the velocity of which is drift velocity can be found out by the component of the river flow along the direction of streaming. To minimize the drift, the net velocity of the boat should be perpendicular to the velocity of the river.

Formula used:
Drift velocity along the minimum drifting i.e.direction of boat perpendicular to the streaming flow is given as,
${{{V}}_{\text{d}}}{{ = (vcos\theta + u)t}}$
Where, ${{\text{V}}_{\text{d}}}$ is the drift velocity, ${{vcos\theta }}$ is the velocity in the direction of minimum drift, $u$ is the initial velocity, $t$ is the time of travel.

Complete answer:
We are interested to find out the value of $x$. Let u be the stream velocity and let v is the velocity of the boat concerning water.
Now, Let the relative velocity of the boat as $v m/s$ which is making an angle of $\theta$ with the vertical (flow direction), and let the velocity of the river as $u$. Let $y$ be the width of the river as shown in the figure below.

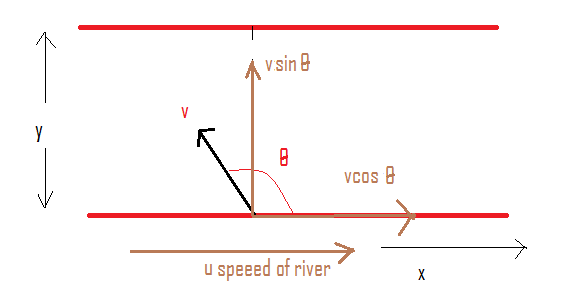
From the formula of speed, the time taken to cross the river is given can be calculated as follows,
${\text{speed = }}\dfrac{{{\text{distance}}}}{{{\text{time}}}}{\text{ = }}\dfrac{{\text{d}}}{{\text{t}}}$
The v makes the angle $\theta$ with the direction of the flow of the river . As we are interested in the velocity of the flow in a horizontal direction thus we are considering the $\sin \theta$component of the velocity.
Using the above diagram, the time is taken’ to cross the river. The $t$ can be represented as
$t = \dfrac{y}{{v\sin \theta }}$ (1)
Now, let us write the drift velocity of both for the given time $t$. The drifting of the boat can be given as,
${{\text{V}}_{\text{d}}}{{ = (vcos\theta + u)t}}$
Put values for the $t$, from the equation given above we get,
$\Rightarrow {v_d} = \left( {u + v\cos \theta } \right) \times \dfrac{y}{{v\sin \theta }}$
Let us simplify it. We get,
$\Rightarrow {v_d} = u(\dfrac{y}{{v\sin \theta }}) + v\cos \theta (\dfrac{y}{{v\sin \theta }})$
Since $\cot \theta = \dfrac{{\cos \theta }}{{\sin \theta }}$ , $\cos ec\theta = \dfrac{1}{{\sin \theta }}$ and we get,
$\Rightarrow {v_d} = \dfrac{u}{v}y\cos ec\theta + y\cot \theta$
Here in the problem we are given as, u/v=n=2, thus substitute the values in the equation of drift velocity, we get,
$\Rightarrow {v_d} = 2y\cos ec\theta + y\cot \theta$ (2)
Now, We have to find the minimum value of drift velocity, to calculate the minimum values first we have to differentiate it for angle and then equate it to zero. As shown below,
$\Rightarrow \dfrac{{d{v_d}}}{{d\theta }} = 2y\dfrac{d}{{d\theta }}\left( {\cos ec\theta } \right) + y\dfrac{d}{{d\theta }}\left( {\cot \theta } \right) = 0$
Since, a derivative of trigonometric formulas are, $\dfrac{d}{{dx}}\left( {\cos ecx} \right) = - \cos ecx\cot x$ and $\dfrac{d}{{dx}}\left( {\cot x} \right) = - \cos e{c^2}x$
On substituting values we get,
$\Rightarrow \dfrac{{d{v_d}}}{{d\theta }} = 2y\left( { - \cos ec\theta \cot \theta } \right) + y\left( { - \cos e{c^2}\theta } \right) = 0 \\\ \Rightarrow 2y\left( { - \cos ec\theta \cot \theta } \right) = y\left( {\cos e{c^2}\theta } \right) \\\$
Let us simplify it. We get,
$\Rightarrow 2y\left( { - \cos ec\theta \cot \theta } \right) = y\left( {\cos e{c^2}\theta } \right)$
Since we know that, $\cos ec\theta = \dfrac{1}{{\sin \theta }},\cot \theta = \dfrac{{\cos \theta }}{{\sin \theta }}$, we get

$$\Rightarrow 2y\left( { - \dfrac{1}{{\sin \theta }}\dfrac{{\cos \theta }}{{\sin \theta }}} \right) = y\left( {\dfrac{1}{{{{\sin }^2}\theta }}} \right) \\\ \\\$$

Let's cancel out they from LHS and RHS, we get
$\Rightarrow 2\left( { - \dfrac{1}{{\sin \theta }}\dfrac{{\cos \theta }}{{\sin \theta }}} \right) = \left( {\dfrac{1}{{{{\sin }^2}\theta }}} \right)$
Let's cancel out the ${\sin ^2}\theta$ from LHS and RHS we get,
$\Rightarrow 2\left( { - \cos \theta } \right) = 1$
$\Rightarrow \cos \theta = \dfrac{{ - 1}}{2} \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{{ - 1}}{2}} \right)$
Let us find the angle for which cosine gives $\dfrac{-1}{2}$.
The angle is , $\theta = {120^o}$ (3)
Now the angle given in the question is $(120+ x)$ and we want to find the value of $x$ we get, (4)
Let us compare equations (3) and (4) and we get the value of $x$ as below.
$\Rightarrow 120 = 120 + x$
$\Rightarrow x = 120 - 120$
$\Rightarrow x = {0^0}$

$\therefore$ The required value of $x$ is zero.

Note:
To calculate the minimum or maximum values of a quantity, we first differentiate it and then equate it to zero.
In this way, we find either the maximum or minimum values.
To check whether the values are maxima or minima we again find it’s the second derivative.