Question

A boat moves relative to water with a velocity half of the river flow velocity. If the angle from the direction of flow at which the boat must move relative to stream directly to minimize drift is $\dfrac{2\pi }{n}$, then find n

Answer 1

In the question we are given the relationship between the velocity of the flow of the river and the velocity of a boat in the river. We are also given the value of the angle made by the boat with the vertical to minimize drift; we need to find the unknown value in the angle. To find this we need to solve for the angle made by the boat with vertical; for that, we need to draw the diagrammatic representation of the given situation and find the components of velocity. Later by applying the condition for minimum drift we can find the solution.
Formula used:
Time for the boat to cross the river,
$t=\dfrac{d}{{{v}_{y}}}$
For minimum drift,
$\dfrac{dx}{d\theta }=0$

Complete step-by-step solution:
In the question, it is said that the velocity of a boat in the water is half of the velocity of the flow of the river.
Consider the figure below.

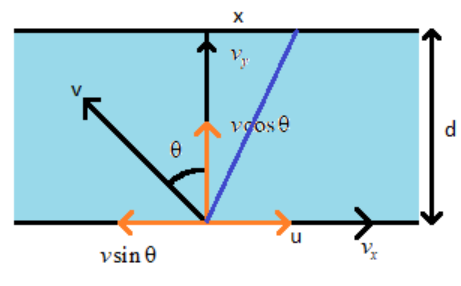
In the figure, ‘d’ is the width of the river, ‘v’ is the velocity of the boat, ‘u’ is the velocity of the river, and ‘$\text{ }\\!\\!\theta\\!\\!\text{ }$’ is the angle at which the boat must move to minimize drift.
We can solve the components of the velocity of the river and the velocity of the boat.
Since it is said in the question that the velocity of the boat is half the velocity of the river, we can write that,
$u=2v$
From the given figure, we can see that the velocity in the x-direction,
${{v}_{x}}=u-v\sin \theta$, since $u$ and $v\sin \theta$ acts along the x-direction opposite to each other.
Since $u=2v$, we have,
${{v}_{x}}=2v-v\sin \theta$
From the figure, we also get that
${{v}_{y}}=v\cos \theta$, because $v\cos \theta$ acts along the y direction.
Let ‘t’ be the time taken by the boat to cross the river.
Then we have time taken by the boat to cross the river,
$\begin{aligned} & t=\dfrac{d}{{{v}_{y}}} \\\ & \Rightarrow t=\dfrac{d}{v\cos \theta } \\\ \end{aligned}$
Let us assume that the boat is drifted by ‘x’ units.
Then the drifting distance will be the product of time taken by the boat and the horizontal component of velocity, i.e.
$\begin{aligned} & x={{v}_{x}}t \\\ & \Rightarrow x=\left( 2v-v\sin \theta \right)\left( \dfrac{d}{v\cos \theta } \right) \\\ \end{aligned}$
In the question it is said that we have to minimize drift.
We know that for minimum drift,
$\dfrac{dx}{d\theta }=0$
By applying this condition, we can write
$\begin{aligned} & \dfrac{dx}{d\theta }=0 \\\ & \Rightarrow \dfrac{d}{d\theta }\left[ \dfrac{d\left( 2v-v\cos \theta \right)}{v\cos \theta } \right]=0 \\\ & \Rightarrow \dfrac{d}{d\theta }\left[ \dfrac{2vd}{v\cos \theta } \right]-\dfrac{d}{d\theta }\left( \dfrac{d\sin \theta }{\cos \theta } \right)=0 \\\ \end{aligned}$
We know that $\dfrac{1}{\cos \theta }=\sec \theta$ and $\dfrac{\sin \theta }{\cos \theta }=\tan \theta$
$\Rightarrow \dfrac{d}{d\theta }\left[ \dfrac{2vd\sec \theta }{v} \right]-\dfrac{d}{d\theta }\left( d\tan \theta \right)=0$
We also know that $\dfrac{d\sec \theta }{d\theta }=\sec \theta \tan \theta$ and $\dfrac{d\tan \theta }{d\theta }={{\sec }^{2}}\theta$
$\Rightarrow \dfrac{2vd}{v}\sec \theta \tan \theta -d{{\sec }^{2}}\theta =0$
By simplifying the above equation, we get
$\begin{aligned} & \dfrac{\Rightarrow 2vd\sec \theta \tan \theta }{v}=d{{\sec }^{2}}\theta \\\ & \Rightarrow 2d\sec \theta \tan \theta =d{{\sec }^{2}}\theta \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow 2d\tan \theta =\dfrac{d{{\sec }^{2}}\theta }{d\sec \theta } \\\ & \Rightarrow 2\tan \theta =\sec \theta \\\ \end{aligned}$
We can replace $\tan \theta$ with $\dfrac{\sin \theta }{\cos \theta }$ and $\sec \theta$ with $\dfrac{1}{\cos \theta }$
Therefore,
$\begin{aligned} & \Rightarrow 2\dfrac{\sin \theta }{\cos \theta }=\dfrac{1}{\cos \theta } \\\ & \Rightarrow 2\sin \theta =1 \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow \sin \theta =\dfrac{1}{2} \\\ & \Rightarrow \theta ={{\sin }^{-1}}\left( \dfrac{1}{2} \right) \\\ \end{aligned}$
We know ${{\sin }^{-1}}\left( \dfrac{1}{2} \right)={{30}^{o}}$
$\Rightarrow \theta ={{30}^{o}}=\dfrac{2\pi }{3}$
In the question we are given that the angle, $\theta =\dfrac{2\pi }{n}$
By calculation we got, $\theta =\dfrac{2\pi }{3}$
By comparing these two, we get n=3.
Therefore the value of ‘n’ is 3.

Note: By solving for the angle for minimum drift, we get
$\theta ={{30}^{o}}$
This angle is given in degrees.
To convert that into radian, first we need to find ${{\theta }^{'}}$
${{\theta }^{'}}={{90}^{o}}+{{30}^{o}}={{120}^{o}}$
This is the angle made with the direction of the flow of the river.
For converting this into radian we need to multiply this with $\dfrac{\pi }{180}$
Therefore,
$\begin{aligned} & {{\theta}^{'}} =120\dfrac{\pi }{180} \\\ & {{\theta}^{'}} =\dfrac{2\pi }{3} \\\ \end{aligned}$
Hence n = 3.