Question

A boat moves relative to water with a velocity half of the river flow velocity if the angle from the direction of flow with which boat must move relative to stream directly to minimize drift is $\dfrac{{2 \times \pi }}{n}$, then n is:
$\left( A \right)$ 1
$\left( B \right)$ 0
$\left( C \right)$ 4
$\left( D \right)$ 3

Answer 1

Hint – Draw the diagrammatic representation, with the velocity of the river be u (moving in R.H.S direction) and the velocity of the boat be v making an angle $\theta$ with perpendicular joining two ends of the rivers or an angle of ${90^o} + \theta$ with the initial velocity of the river. Let the width of the river be (d) meters, resolve the velocity into its components and use the concept that drifting distance is equal to the time taken by the boat and the horizontal component of the velocity. This will help approaching the problem.

Complete step-by-step answer:

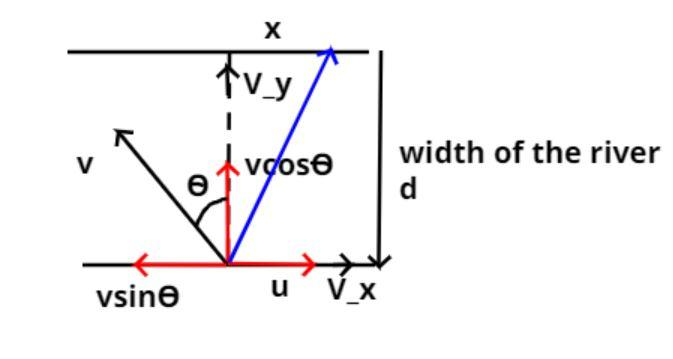
Let the velocity of the river be u (moving in R.H.S direction) and the velocity of the boat be v as shown in the figure.
Let the boat start moving in the river from point A, it did not reach to point B which is vertically opposite to point A because of the velocity of the river.
To minimize the drift we have to row the boat at an angle $\theta$ with the vertical as shown in the figure.
So the angle $\left( {\theta '} \right)$ boat makes with the positive direction of x axis is, $\theta ' =$ ${90^0} + \theta$............. (1)
Let the width of the river be (d).
Now the components of the velocity in the x and y axis are $v\sin \theta$ and $v\cos \theta$ as shown in the figure.
So the vertical velocity component is ${V_y} = v\cos \theta$
And the horizontal velocity component is ${V_x} = u - v\sin \theta$
Let the time taken by the boat to cross the river be (t).
So the time taken by the boat is = $t = \dfrac{d}{{{V_y}}}$
$\Rightarrow t = \dfrac{d}{{v\cos \theta }}$....................... (2)
Now let the boat be drifted by x units as shown in the figure.
So this drifting distance is equal to the time taken by the boat and the horizontal component of the velocity.
$\Rightarrow x = t.{V_x}$
$\Rightarrow x = \dfrac{d}{{v\cos \theta }}\left( {u - v\sin \theta } \right)$
Now we have to minimize this drift and find out the value of the angle the boat makes with the positive direction of the x axis.
So differentiate it w.r.t $\theta$ and equate to zero we have,
$\Rightarrow \dfrac{d}{{d\theta }}x = \dfrac{d}{{d\theta }}\left[ {\dfrac{d}{{v\cos \theta }}\left( {u - v\sin \theta } \right)} \right] = \dfrac{d}{{d\theta }}\left[ {\dfrac{{ud}}{{v\cos \theta }}} \right] - \dfrac{d}{{d\theta }}\left( {d\dfrac{{\sin \theta }}{{\cos \theta }}} \right) = 0$
Now as we know that $\dfrac{1}{{\cos \theta }} = \sec \theta {\text{ and }}\dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta$ so we have,
$\Rightarrow \dfrac{d}{{d\theta }}x = \dfrac{d}{{d\theta }}\left[ {\dfrac{{ud\sec \theta }}{v}} \right] - \dfrac{d}{{d\theta }}\left( {d\tan \theta } \right) = 0$
Now differentiate it according to property $\dfrac{d}{{d\theta }}\sec \theta = \sec \theta \tan \theta {\text{ and }}\dfrac{d}{{d\theta }}\tan \theta = {\sec ^2}\theta$ so we have,
$\Rightarrow \dfrac{d}{{d\theta }}x = \dfrac{{ud}}{v}\sec \theta \tan \theta - d{\sec ^2}\theta = 0$
Now simplify this we have,
$\Rightarrow \dfrac{{ud}}{v}\sec \theta \tan \theta = d{\sec ^2}\theta$
$\Rightarrow \dfrac{u}{v}\tan \theta = \sec \theta$
$\Rightarrow \dfrac{u}{v}\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{{\cos \theta }}$
$\Rightarrow \sin \theta = \dfrac{v}{u}$
$\Rightarrow \theta = {\sin ^{ - 1}}\left( {\dfrac{v}{u}} \right)$.................... (2)
Now it is given that the velocity of the boat is half of the velocity of the river.
$\Rightarrow v = \dfrac{1}{2}u$
So substitute this value in equation (2) we have,
$\Rightarrow \theta = {\sin ^{ - 1}}\left( {\dfrac{{\dfrac{1}{2}u}}{u}} \right) = {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) = {\sin ^{ - 1}}\left( {\sin {{30}^0}} \right) = {30^0}$
Now from equation (1) we have,
$\Rightarrow \theta ' = {90^o} + {30^o} = {120^o}$
Now convert this into radian by multiplying $\dfrac{\pi }{{{{180}^0}}}$ so we have,
$\Rightarrow \theta ' = {120^o} \times \dfrac{\pi }{{{{180}^o}}} = \dfrac{{2 \times \pi }}{3}$
Now compare this drift with the given drift we have,
$\Rightarrow \dfrac{{2 \times \pi }}{n} = \dfrac{{2 \times \pi }}{3}$
So on comparing n = 3.
So this is the required answer.

Hence option (D) is the correct answer.

Note – Since the drift has to be minimized therefore we have differentiated the drifting distance w.r.t $\theta$ and equate to zero. This gives the value of $\theta$ in terms of the velocities of boat and the river. Using the specific relation between speed of boat and the river $\theta$ can be obtained. Now we have computed ${90^o} + \theta$, because the question asks that the angle from the direction of flow with which boat must move relative to stream to minimize drift.