Question

A boat crosses a river of width $200\,{\text{m}}$ in the shortest time and is found to experience a drift of $100\,{\text{m}}$ in reaching the opposite bank. The time taken is now ‘t’. If the same boat is to cross the river by the shortest path, the time taken to cross will be:
A. $2t$
B. $\sqrt 2 t$
C. $3t$
D. $\dfrac{{2t}}{{\sqrt 3 }}$

Answer 1

Use the formula for velocity of an object. Write the equation for velocity of the boat and velocity of the river. Then draw the diagram representing the velocities of the river and boat. Then from this diagram determine the resultant velocity of the boat to cross the river. Hence, determine the time required to cross the river.

Formula used:
The velocity $v$ of an object is given by
$v = \dfrac{s}{t}$ …… (1)
Here, $s$ is the displacement of the object and $t$ is time.

Complete step by step answer:
We have given that the width of the river is $200\,{\text{m}}$ and drift experienced by the boat is $100\,{\text{m}}$.
$w = 200\,{\text{m}}$
$\Rightarrow d = 100\,{\text{m}}$
The time taken by the boat to cross the river is $t$. We have asked to determine the time taken by the boat to cross the river by the shortest path.Let ${v_R}$ and ${v_B}$ be the velocities of the river and boat.According to equation (1), the velocity of the boat to cross the river by shortest path is
${v_B} = \dfrac{{200\,{\text{m}}}}{t}$ …… (2)
The boat experiences the drift due to velocity of the river given by
${v_R} = \dfrac{{100\,{\text{m}}}}{t}$

Let us now draw the diagram showing the velocities of the boat and river.

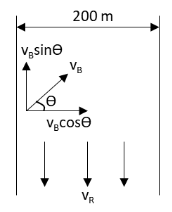
From the above diagram, we can see that the velocity of the river gets cancelled by the vertical component of velocity of the boat.
${v_R} = {v_B}\sin \theta$
Substitute $\dfrac{{100\,{\text{m}}}}{t}$ for ${v_R}$ and $\dfrac{{200\,{\text{m}}}}{t}$ for ${v_B}$ in the above equation.
$\dfrac{{100\,{\text{m}}}}{t} = \dfrac{{200\,{\text{m}}}}{t}\sin \theta$
$\Rightarrow \sin \theta = \dfrac{1}{2}$
$\Rightarrow \theta = 30^\circ$
The velocity $v$ of the boat while crossing the river by shortest path is the horizontal component of velocity of the boat ${v_B}\cos \theta$.
$v = {v_B}\cos 30^\circ$
From equation (2). We can write
$t' = \dfrac{{200\,{\text{m}}}}{v}$
Here, $t'$ is the time required to cross the river.
Substitute ${v_B}\cos 30^\circ$ for $v$ in the above equation.
$t' = \dfrac{{200\,{\text{m}}}}{{{v_B}\cos 30^\circ }}$
Substitute $\dfrac{{200\,{\text{m}}}}{t}$ for ${v_B}$ in the above equation.
$t' = \dfrac{{200\,{\text{m}}}}{{\dfrac{{200\,{\text{m}}}}{t}\cos 30^\circ }}$
$\Rightarrow t' = \dfrac{{200\,{\text{m}}}}{{\dfrac{{200\,{\text{m}}}}{t}\dfrac{{\sqrt 3 }}{2}}}$
$\therefore t' = \dfrac{{2t}}{{\sqrt 3 }}$
Therefore, the time required for the boat to cross the river by shortest path is $\dfrac{{2t}}{{\sqrt 3 }}$.

Hence, the correct option is D.

Note: The students should keep in mind the velocity of the river causes the boat to experience the drift. Hence, one should not forget to consider the velocity of the river and this drift of the boat. Also the students should keep in mind that the vertical component of velocity of the boat gets cancelled with velocity of the river. Hence, the only velocity of the boat is its horizontal component.