Question

A boat covers a certain distance downstream in 8 hours and the same distance upstream in 10 hours. If the speed of the current is 1 km/hr, then find the distance of the one way journey.km
[a] 60 km/hr
[b] 70 km/hr
[c] 80 km/hr
[d] 90 km/hr.

Answer 1

Hint: Assume the distance covered be x and the speed of the boat in still water be y. Using the statement of the question form two linear equations in two variables x and y. Solve the system of equations using elimination method or substitution method or graphically or using matrices. The value of x will give the distance of the one-way journey.

Complete step by step answer:
Let the distance of the one-way journey be x, and the speed of the boat in still water be y.
Speed of the boat downstream = y+1
Using $\text{speed}=\dfrac{\text{Distance covered}}{\text{Time taken}}$
Hence the time taken to cover a one-way journey downstream $=\dfrac{x}{y+1}$ hours.
But given that the time taken to cover one-way journey downstream = 8 hours, we have
$\begin{aligned} & \dfrac{x}{y+1}=8 \\\ & \Rightarrow x=8y+8\text{ (i)} \\\ \end{aligned}$
Speed of the boat upstream = y-1
Using $\text{speed}=\dfrac{\text{Distance covered}}{\text{Time taken}}$
Hence the time taken to cover a one-way journey upstream $=\dfrac{x}{y-1}$ hours.
But given that the time taken to cover one-way journey upstream = 10 hours, we have
$\begin{aligned} & \dfrac{x}{y-1}=10 \\\ & \Rightarrow x=10y-10\text{ (ii)} \\\ \end{aligned}$
Substituting the value of x from equation (i) in equation (ii), we get
8y+8 = 10y-10
Subtracting 8y from both sides, we get
8 = 2y-10
Adding 10 on both sides, we get
18 =2y
Dividing both sides by 2, we get
y=9.
Substituting the value of y in equation (i), we get
x = 72+8 = 80
Hence the distance of one-way journey = 80 Km
Hence option [c] is correct.

Note: Plotting the given system of equations graphically.
The graph of the system of equations is shown below.

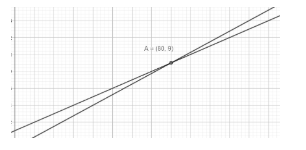
As is evident from the graph the given system of equations intersect at the point (80,9)
Hence x = 80 and y = 9 is the solution of the given system, which is the same as obtained above.