Question

A block X of mass $0.5\;kg$ is held by a long massless string on a frictionless inclined plane of inclination $30{}^\circ$ to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass $2\;kg$ and of radius $0.2\;m$ as shown in figure. The drum is given an initial angular velocity such that block X starts moving up the plane. At a certain instant of time, the magnitude of the angular velocity of Y is $10rad{{s}^{-1}}$ . Calculate the distance (in $m$ ) travelled by X from that instant of time until it comes to rest. Round off to the closest integer. $\left[ g=10m{{s}^{-2}} \right]$

Answer 1

The net force acting on the block is due to the tensional force by the string and the gravitational force. From this the acceleration of the block can be obtained. From the remaining given values, by using the equations for uniformly accelerated motion, we can find the distance travelled.

Complete step by step answer:
Let us note down the given data;
Mass of the block $m=0.5kg$
Angle of inclination of the block $\theta =30{}^\circ$
Mass of the cylindrical drum $M=2kg$
Radius of the cylindrical drum $R=0.2m$
Angular velocity of the rotating drum $\omega =10rad{{s}^{-1}}$
Now, an initial angular velocity is provided to the cylindrical drum. Due to this the string connecting drum and block gets stretched and creates tension. Due to this tension the block starts moving upward. However, this motion is opposed by the gravitational force.
As the plane is inclined, we have to take the component of the vertically downward gravitational force in the direction opposite to the motion.
The forces acting on the system and its components can be shown as below;

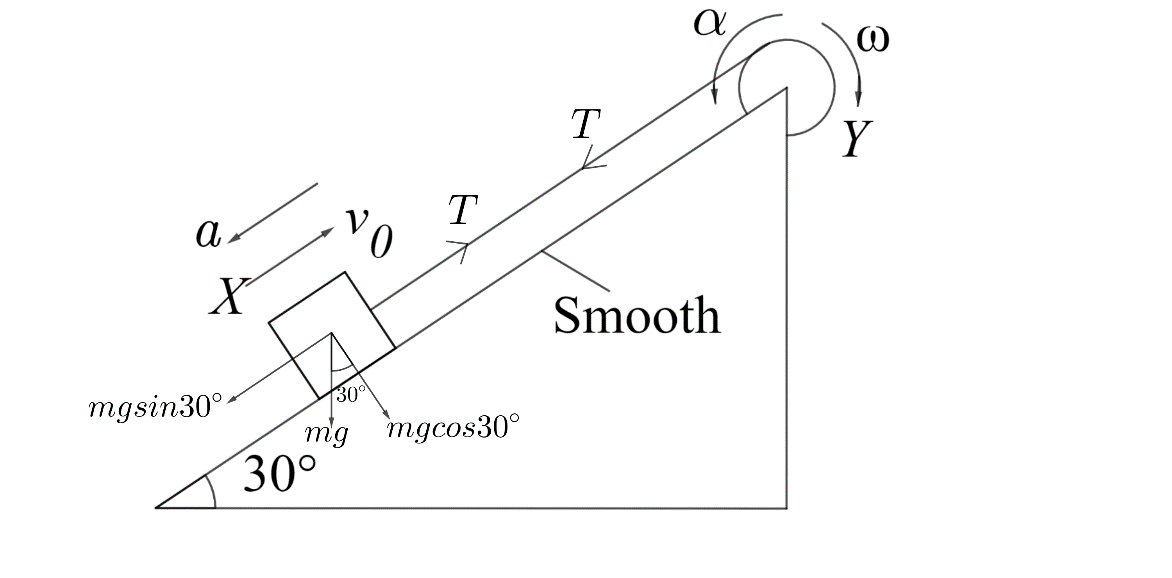
Now, the motion of the block is the resultant of the tension of the string and the gravitational force, where the tension of the string has to be greater than the gravitational force.
Hence, the resultant force is expressed as;
$T-mg\sin 30{}^\circ =ma$ , where $a$ is the acceleration of the block.
$\therefore T=ma+\dfrac{mg}{2}$ …… $(1)$
Now, the tension of the string also causes retarding torque on the cylindrical drum, which is balanced by the rotational torque of the drum.
We know that torque is the product of the force acting on the object and the distance of force acting from the centre.
Hence, the torque due to the string can be expressed as,
$\tau =TR$ …… $(2)$
This torque is balanced by the rotational force, which is given by
$\tau =I\alpha$ …… $(3)$
where $I$ is the moment of inertia
$\alpha$ is the angular acceleration
The moment of inertia for drum is,
$I=\dfrac{M{{R}^{2}}}{2}$ …… $(4)$
We know that the linear acceleration is the product of the angular acceleration and the radius of the object.
$\therefore \alpha =\dfrac{a}{R}$ …… $(5)$
Substituting the values of the equation $(3)$ , $(4)$ , and $(5)$ in the equation $(2)$
$\therefore TR=\left( \dfrac{M{{R}^{2}}}{2} \right)\left( \dfrac{a}{R} \right)$
$\therefore T=\dfrac{aM}{2}$
As this tension is acting in the opposite direction
$\therefore T=-\dfrac{aM}{2}$ …… $(6)$
Comparing equations $(1)$ and $(6)$
$\therefore ma+\dfrac{mg}{2}=-\dfrac{aM}{2}$
Taking LCM on both sides,
$\therefore 2ma+mg=-aM$
$\therefore 2ma+aM=mg$
Making acceleration the subject of the equation,
$\therefore a=\dfrac{mg}{M+2m}$
Substituting the given values,
$\therefore a=\dfrac{(0.5)(10)}{2+2(0.5)}$
$\therefore a=\dfrac{5}{3}m{{s}^{-2}}$
As the motion is retarding, we have to take negative sign before acceleration,
$\therefore a=-\dfrac{5}{3}m{{s}^{-2}}$
Now, the linear initial velocity is given as,
$u=\omega R$
Substituting the given values,
$u=(10)(0.2)$
$\therefore u=2m{{s}^{-1}}$
As the block finally comes to rest,
$v=0m{{s}^{-1}}$
Substituting all these values in the equation of uniformly accelerated motion
${{v}^{2}}-{{u}^{2}}=2as$
$\therefore {{(0)}^{2}}-{{(2)}^{2}}=2(-\dfrac{5}{3})s$
Hence, the distance travelled is,
$\therefore s=\dfrac{12}{10}m$
$\therefore s\approx 1m$ .

Note:
Here, we have to take the sign of the acceleration to be negative, as the motion is retarding and the block comes to rest at the end. Here, we are given that the surface is smooth, hence we can ignore the frictional force. Else we have to include the frictional force acting on the block in the opposite direction of motion i.e. in the downward direction.